CHAPTER 25
GENERATING PHRASES IN ANOTHER LANGUAGE
Following are new notations for expressing phrase generation.
They may be used within semantic specifications to generate phrases
in another language.
These notations let you, the programmer, specify translations
~oblivious ~to ~the ~existence ~of ~any ~ambiguity ~at ~all. Ambiguity
is supported implicitly, and delightfully, it's relatively easy to
implement. We will see the implementation of each notation after we
present it. (Section 25.5 shows how ambiguities between domains meet).
Our main example has the syntax grammar's semantics generate phrases
in the datatype language. This is how we require that a specification
make sense syntactically ~and within the domain of datatypes.
The next chapter shows the complete specification of syntax rules
whose semantics generate phrases in the datatype language. There,
we will see an implementation of a programming language that involves
datatypes. That implementation will use the notations presented in
this chapter.
25.1
Notation For Generating Unit-Length Phrases
We now introduce notations for the generation of phrases. We've been
using one of the most important of these notations all along. Recall
that a rule is usually specified via the notation:
<POS(1):V(1)> ... <POS(k):V(k)> ->
<GIVE_POS: f(V(1),...,V(k))>
In general, we allow the righthand side of the rule to be a general
program, as in:
<POS(1):V(1)> <POS(2):V(2)> ... <POS(k):V(k)> ->
a program
---------------- Parentheses in previous paragraph mean subscripting! ---
25.2
The Righthand Side Of A Rule Is Always A STATEMENT
In fact, ~the ~righthand ~side ~of ~a ~rule ~is ~always ~a ~STATEMENT.
We've been living with this since Section 1.3. The notation:
<POS: f(...) >
is actually a STATEMENT!
25.2.1
The Righthand-Side Of A Rule Can Naturally Involve IFs
Because the give-phrase notation "<ID:STATEMENT>" is itself a
STATEMENT, we are able to express rules (from Chapter 3) like:
<EXPR[i]:x> <BOP[j]:y> <EXPR[k]:z> ->
IF i =< j & k < j THEN
<EXPR[j]: f(x,y,z) > FI
This rule uses the IF-THEN notation for STATEMENTs. This is perfectly
valid because the "<EXPR:...>" in the THEN clause is a STATEMENT, and
the righthand side of a rule is expected always to be a STATEMENT.
25.3
Phrase Generation Is A STATEMENT Anywhere, Even Beyond Rules' Righthand
Sides
In general, phrase generation STATEMENTs are supported by the rules:
< ID : STATEMENT > -> STATEMENT
< ID [ EXPR ] : STATEMENT > -> STATEMENT
The ID names the part-of-speech. The given STATEMENT specifies
the semantics. These translate ultimately into a call to GIVE
(Section 25.3.3 and Chapter 12).
Each generates a unit-length phrase whose part-of-speech is the ID and
whose semantics is the STATEMENT. We've seen this on the righthand
sides of rules.
The second rule here is for specifying array parts-of-speech, which
require an index (the EXPR, of type INT) to denote which ~one of the
array of parts-of-speech is intended for the new phrase.
For example, consider the STATEMENT forming the righthand side of the
rule:
<NUMBER:n> -> <EXPR: LOAD( 1, ADDRESS_OF(n) ); >
That STATEMENT:
<EXPR: LOAD( 1, ADDRESS_OF(n) ); >
generates an <EXPR> whose semantics is the STATEMENT within the
"<...>", the:
LOAD( 1, ADDRESS_OF(n) );
25.3.1
Semantics Can Also Be An EXPR
The STATEMENT within the angle-brackets can also be an EXPR, as in:
< ID : EXPR > -> STATEMENT
< ID [ EXPR ] : EXPR > -> STATEMENT
In general, parts-of-speech declared with the dash, e.g.,
POS EXPR : - ;
must be specified using the STATEMENT form inside the "<...>". All
other parts-of-speech, declared like:
POS ID : TEXT ;
where the semantics is a specified datatype, use the EXPR form inside
the "<...>".
The ":STATEMENT" or ":EXPR" may be omitted, as in:
< ID >
In the absence of semantic specification, the default semantics will
do nothing when it might be invoked, and will return 0, FALSE, or NIL
if it is used as a value.
BOX: What notation have we been using all along that
BOX: generates a phrase?
BOX:
BOX: Can this notation be used anywhere that a STATEMENT
BOX: is permissible?
25.3.2
The STATEMENT or EXPR Inside The "<...>" Is Rendered As A Process
Recall from Chapter 4 that we implicitly enclose any semantic
specification within the "//...\\" to render it as a process. This
was done to render all semantics as ~delayed semantics, so that ~no
semantics would be executed during the parsing action.
We implement that delaying transformation here.
When we specify (e.g., on the righthand side of a rule):
< POS : f(x,y,z) >
we actually deliver:
< POS : //[x;y;z;] f( <*x*>, <*y*>, <*z*> ) \\ >
The variables enclosed in the "//[...]", the context variables X, Y,
and Z, come from the lefthand part of a rule, the want-phrase. The
"//[...]" and "\\" are implicit. This delays the invocation of f.
Also, each appearence of those context variables in the body is
enclosed by the process invocation notation "<*...*>" if needed.
This ~undelays the delayed semantics associated with the variables
X, Y, and Z.
25.3.3
The Translation Of The "<...>" Into A Call To GIVE
The STATEMENT:
< ID : STATEMENT >
always translates to:
GIVE( [ LEFT:LEFT POS:ID SEM: //[...] STATEMENT \\ ] );
This is a full call to GIVE, like we saw in Chapter 15.
Beyond the given ID (part-of-speech) and STATEMENT (semantics), the
global variable ~LEFT is read.
LEFT is one of the variables read implicitly by the "<...>" notation.
Once GIVE is called, GIVE reads and writes the variable C as well,
even though we don't pass it in here (see Section 12.3 or 15.2.1).
LEFT and C are thus read implicitly by the STATEMENT:
< ID : STATEMENT >
The following introduces ways to manage these two implicit variables.
BOX: BOX: What does the phrase generation notation "<...>"
BOX: translate into?
BOX:
BOX: Could the righthand side of a rule consist of WHILE
BOX: statements, among other things?
BOX:
BOX: How has an IF statement on the righthand side been
BOX: helpful?
BOX:
BOX: How is Chapter 4's implicit delayed semantics
BOX: implemented?
25.4
The Two Endpoints Of Generated Phrases: The Global Variables LEFT and C
Whenever a phrase is generated, whether it be on the righthand side
of a rule, or as any action, two global variables define the
left and right endpoints for the new phrase.
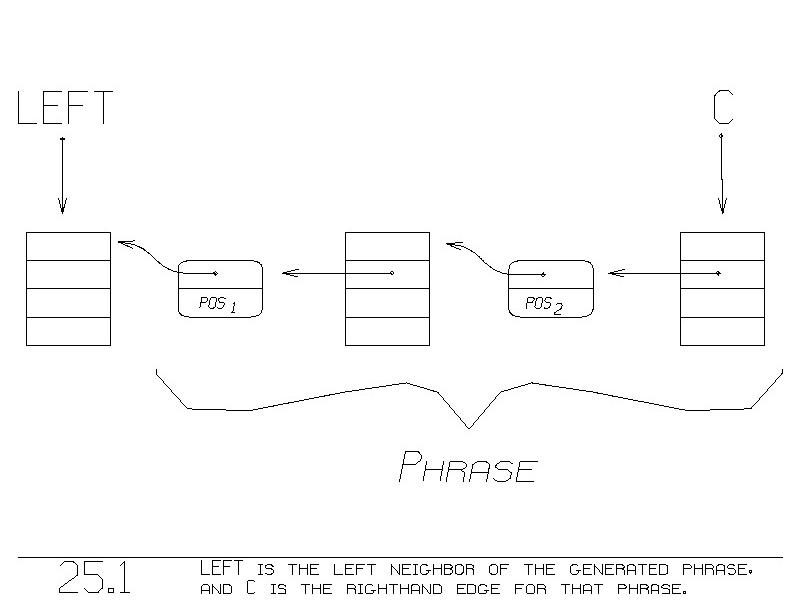 LEFT, a CHOICE_OF_PHRASES, denotes the left neighbor for a generated
phrase. The variable C, also a CHOICE_OF_PHRASES, denotes the
righthand edge for the generated phrase. Figure 25.1 illustrates this.
The "<...>" notation, the GIVE, reads these two variables implicitly.
Thus, the values in those two variables are important whenever we
see a "<...>".
How are these variables set?
25.4.1
A Rule's Want-Phrase Sets LEFT
LEFT is set upon matching a want-phrase. Recall that a rule:
<POS(1)> <POS(2)> ... <POS(k)> -> some_action
is turned into a program via the following (from the end of Section
12.3.3). P is the PHRASE block passed to GIVE (and the grammar):
P(k):= P ;
IF P(k).POS = POS(k) THEN
FOR P(k-1) $E P(k).LEFT; WITH P(k-1).POS = POS(k-1) ;
!!
...
!!
FOR P(1) $E P(2).LEFT; WITH P(1).POS = POS(1);
DO
~LEFT:= ~P(1).LEFT;
some_action
END
FI
The "some_action" is executed in a context where LEFT points to the
matched phrase's lefthand neighbor.
---------------- Parentheses in previous paragraph around "1", "2"
---------------- "k", and "k-1" mean subscripting! ---------------------
The action is usually:
GIVE( [ LEFT: LEFT POS: the_righthand_part_of_speech
SEM: //...\\ ] );
This is so if the righthand side of the rule is of the form:
< ID : STATEMENT >
This action now executes in the context where LEFT is the lefthand
neighbor of the matched want-phrase. As always, C holds the rightmost
PHRASE block of the matched phrase (Section 12.3.1).
GIVE will put the newly generated phrase's rightmost block also onto
C. Thus, the newly generated unit-length phrase ~shares ~the ~same
~span (LEFT and C) with the matched want-phrase.
BOX: What do the variables LEFT and C signify?
BOX:
BOX: Why does the generated give-phrase (in a context-free
BOX: rule) share the same span with the matched occurence
BOX: of the rule's want-phrase?
25.4.2
Phrases Of Length Greater Than One
The treatment of the global variables LEFT and C that we saw with
general rewrite rules (Section 12.5) and the taking of user input
(Section 12.4), are now rendered implicit with a new notation.
25.4.2.1
Brief Notation For Setting LEFT and C
STATEMENTs may be combined in a way other than sequential execution.
The "-" may be used to combine STATEMENTs, as supported by the rule:
STATEMENT - STATEMENT - ... - STATEMENT -> STATEMENT
The dashes deal with the variables LEFT and C. LEFT and C are set
up especially for each of the individual STATEMENTs.
This dash notation is meant to be used for generating phrases of length
greater than one. For example:
<POS(1)> - <POS(2)>
combines with a dash the two STATEMENTS:
<POS(1)> and <POS(2)>
This forms a phrase of length two.
---------------- Parentheses in previous paragraph mean subscripting! ---
A general rewrite rule is actually written as:
<POS(1)> ... <POS(k)> -> <GIVE_POS(1)> - ... - <GIVE_POS(n)>
where dashes separate the phrase elements on the righthand side of
the rule. This is our official notation for general rewrite rules
(rather than the dashless notation used in Section 1.3).
---------------- Parentheses in previous paragraph around "1" and "k"
---------------- mean subscripting! -----------------------
How is the rule:
STATEMENT - STATEMENT - ... - STATEMENT -> STATEMENT
implemented? It translates (see Section 12.5) to the following.
(Back there, each STATEMENT was a call to GIVE):
HOLDING LEFT; "(Preserve LEFT so that it looks like we never
modified it)"
DO
RIGHTHAND:= C; "Remember present C, for our final
STATEMENT"
C:= NIL; ~STATEMENT(1)
LEFT:= C; C:= NIL; ~STATEMENT(2)
LEFT:= C; C:= NIL; ~STATEMENT(3)
...
LEFT:= C; C:= NIL; ~STATEMENT(n-1)
LEFT:= C; C:= RIGHTHAND; ~STATEMENT(n)
ENDHOLD
Assuming that each of the STATEMENTs is of the form:
< ID : STATEMENT >
then the overall effect is to generate the entire phrase (connected
by dashes) with LEFT as its left neighbor, where the rightmost phrase
block is appended onto C.
---------------- Parentheses in previous paragraph around "1", "2"
---------------- "3", and "n" and "n-1"" mean subscripting! ------------
That is, where we wrote:
< ID : STATEMENT >
to generate a phrase of length one, spanning from LEFT to C, we can now
write:
<ID : STATEMENT> - <ID : STATEMENT> - ... - <ID : STATEMENT>
to generate a phrase of length greater than one, also spanning from
LEFT to C.
NOTE: STATEMENTs connected with dashes bind together ~before
STATEMENTs separated by nothing (our usual way for putting
STATEMENTs together). Thus,
<A> <B> <C> - <D> <E>
groups as:
<A> <B> (<C> - <D>) <E>
Also:
<A> - <B> <C> - <D> - <E> <F> - <G>
groups as:
(<A> - <B>) (<C> - <D> - <E>) (<F> - <G>)
BOX: BOX: How do you combine STATEMENTs so as to generate a
BOX: phrase of length greater than one?
BOX:
BOX: Is the implementation identical to how we generate
BOX: the give-phrase of a general rewrite rule?
25.4.3
Ambiguous Phrase Generation: Phrase Generation Without The Dashes
LEFT, a CHOICE_OF_PHRASES, denotes the left neighbor for a generated
phrase. The variable C, also a CHOICE_OF_PHRASES, denotes the
righthand edge for the generated phrase. Figure 25.1 illustrates this.
The "<...>" notation, the GIVE, reads these two variables implicitly.
Thus, the values in those two variables are important whenever we
see a "<...>".
How are these variables set?
25.4.1
A Rule's Want-Phrase Sets LEFT
LEFT is set upon matching a want-phrase. Recall that a rule:
<POS(1)> <POS(2)> ... <POS(k)> -> some_action
is turned into a program via the following (from the end of Section
12.3.3). P is the PHRASE block passed to GIVE (and the grammar):
P(k):= P ;
IF P(k).POS = POS(k) THEN
FOR P(k-1) $E P(k).LEFT; WITH P(k-1).POS = POS(k-1) ;
!!
...
!!
FOR P(1) $E P(2).LEFT; WITH P(1).POS = POS(1);
DO
~LEFT:= ~P(1).LEFT;
some_action
END
FI
The "some_action" is executed in a context where LEFT points to the
matched phrase's lefthand neighbor.
---------------- Parentheses in previous paragraph around "1", "2"
---------------- "k", and "k-1" mean subscripting! ---------------------
The action is usually:
GIVE( [ LEFT: LEFT POS: the_righthand_part_of_speech
SEM: //...\\ ] );
This is so if the righthand side of the rule is of the form:
< ID : STATEMENT >
This action now executes in the context where LEFT is the lefthand
neighbor of the matched want-phrase. As always, C holds the rightmost
PHRASE block of the matched phrase (Section 12.3.1).
GIVE will put the newly generated phrase's rightmost block also onto
C. Thus, the newly generated unit-length phrase ~shares ~the ~same
~span (LEFT and C) with the matched want-phrase.
BOX: What do the variables LEFT and C signify?
BOX:
BOX: Why does the generated give-phrase (in a context-free
BOX: rule) share the same span with the matched occurence
BOX: of the rule's want-phrase?
25.4.2
Phrases Of Length Greater Than One
The treatment of the global variables LEFT and C that we saw with
general rewrite rules (Section 12.5) and the taking of user input
(Section 12.4), are now rendered implicit with a new notation.
25.4.2.1
Brief Notation For Setting LEFT and C
STATEMENTs may be combined in a way other than sequential execution.
The "-" may be used to combine STATEMENTs, as supported by the rule:
STATEMENT - STATEMENT - ... - STATEMENT -> STATEMENT
The dashes deal with the variables LEFT and C. LEFT and C are set
up especially for each of the individual STATEMENTs.
This dash notation is meant to be used for generating phrases of length
greater than one. For example:
<POS(1)> - <POS(2)>
combines with a dash the two STATEMENTS:
<POS(1)> and <POS(2)>
This forms a phrase of length two.
---------------- Parentheses in previous paragraph mean subscripting! ---
A general rewrite rule is actually written as:
<POS(1)> ... <POS(k)> -> <GIVE_POS(1)> - ... - <GIVE_POS(n)>
where dashes separate the phrase elements on the righthand side of
the rule. This is our official notation for general rewrite rules
(rather than the dashless notation used in Section 1.3).
---------------- Parentheses in previous paragraph around "1" and "k"
---------------- mean subscripting! -----------------------
How is the rule:
STATEMENT - STATEMENT - ... - STATEMENT -> STATEMENT
implemented? It translates (see Section 12.5) to the following.
(Back there, each STATEMENT was a call to GIVE):
HOLDING LEFT; "(Preserve LEFT so that it looks like we never
modified it)"
DO
RIGHTHAND:= C; "Remember present C, for our final
STATEMENT"
C:= NIL; ~STATEMENT(1)
LEFT:= C; C:= NIL; ~STATEMENT(2)
LEFT:= C; C:= NIL; ~STATEMENT(3)
...
LEFT:= C; C:= NIL; ~STATEMENT(n-1)
LEFT:= C; C:= RIGHTHAND; ~STATEMENT(n)
ENDHOLD
Assuming that each of the STATEMENTs is of the form:
< ID : STATEMENT >
then the overall effect is to generate the entire phrase (connected
by dashes) with LEFT as its left neighbor, where the rightmost phrase
block is appended onto C.
---------------- Parentheses in previous paragraph around "1", "2"
---------------- "3", and "n" and "n-1"" mean subscripting! ------------
That is, where we wrote:
< ID : STATEMENT >
to generate a phrase of length one, spanning from LEFT to C, we can now
write:
<ID : STATEMENT> - <ID : STATEMENT> - ... - <ID : STATEMENT>
to generate a phrase of length greater than one, also spanning from
LEFT to C.
NOTE: STATEMENTs connected with dashes bind together ~before
STATEMENTs separated by nothing (our usual way for putting
STATEMENTs together). Thus,
<A> <B> <C> - <D> <E>
groups as:
<A> <B> (<C> - <D>) <E>
Also:
<A> - <B> <C> - <D> - <E> <F> - <G>
groups as:
(<A> - <B>) (<C> - <D> - <E>) (<F> - <G>)
BOX: BOX: How do you combine STATEMENTs so as to generate a
BOX: phrase of length greater than one?
BOX:
BOX: Is the implementation identical to how we generate
BOX: the give-phrase of a general rewrite rule?
25.4.3
Ambiguous Phrase Generation: Phrase Generation Without The Dashes
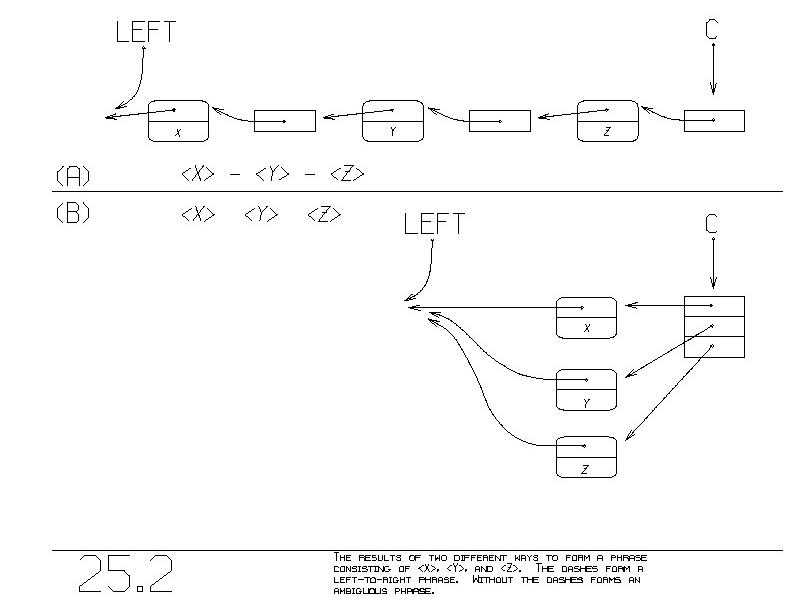 Figure 25.2(a) shows what is built when you execute the statement:
<X> - <Y> - <Z>
Figure 25.2(b) shows what:
<X> <Y> <Z>
generates. With the dashes, we get a left-to-right phrase.
Without the dashes, the three short phrases become one ambiguous
phrase. They all become members of the same CHOICE_OF_PHRASES.
This is natural because the dashless STATEMENT calls GIVE once per
short phrase, without touching C nor LEFT. GIVE puts all its given
phrases onto the same CHOICE_OF_PHRASES, C.
Figure 25.2(a) shows what is built when you execute the statement:
<X> - <Y> - <Z>
Figure 25.2(b) shows what:
<X> <Y> <Z>
generates. With the dashes, we get a left-to-right phrase.
Without the dashes, the three short phrases become one ambiguous
phrase. They all become members of the same CHOICE_OF_PHRASES.
This is natural because the dashless STATEMENT calls GIVE once per
short phrase, without touching C nor LEFT. GIVE puts all its given
phrases onto the same CHOICE_OF_PHRASES, C.
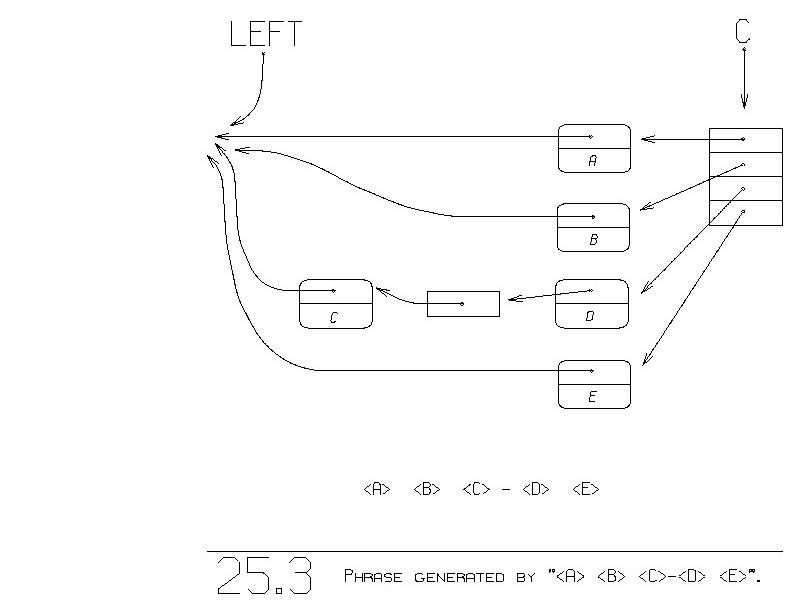 For another example, figure 25.3 shows what is built upon the execution
of:
<A> <B> <C> - <D> <E>
For another example, figure 25.3 shows what is built upon the execution
of:
<A> <B> <C> - <D> <E>
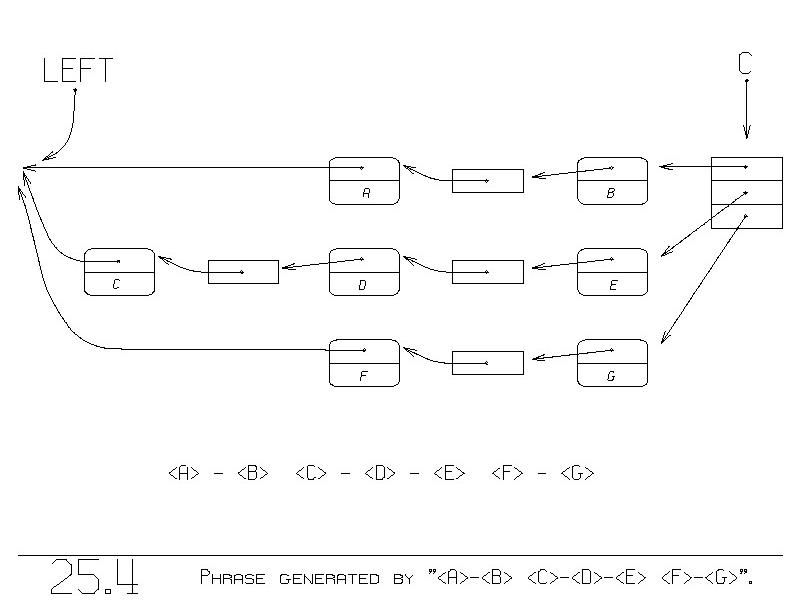 Figure 25.4 shows:
<A> - <B> <C> - <D> - <E> <F> - <G>
Now suppose the procedures X and Y are defined by:
DEFINE X: <A> ENDDEFN
DEFINE Y: <B> - <C> ENDDEFN
The STATEMENT:
X; Y;
generates an ambiguous phrase consisting of the phrase "<A>" and
the phrase "<B><C>". In contrast:
X; - Y;
generates one phrase, "<A><B><C>". (The semicolons are part of the
atomic STATEMENTs, as:
X;
is the notation for calling procedure X). In general, the normal
~sequential execution of phrase generations "<...>" offers up the
phrases as ambiguous, multiple interpretations sharing the same span
(LEFT and C).
We will see examples of phrase generation from within the semantics of
syntax rules in next chapter.
BOX: What kind of phrase is generated by a sequence of
BOX: STATEMENTs without the dashes?
BOX:
BOX: Can phrase generation be packaged in procedures?
25.5
Two Kinds Of Ambiguity At Once - The Passage Of Ambiguity From One Domain
To The Next
Ambiguities can arise from the syntax grammar and also from the
datatype grammar. Both kinds of ambiguity manifest themselves in the
same way. They result in ambiguous datatype phrases.
25.5.1
Datatype Ambiguities
25.5.1.1
Ambiguities From Coercion
Let's first examine ambiguities that arise from the datatype grammar
alone. For example, the phrase:
1
is turned into the datatype phrase:
~INT
The coercion from INT to REAL:
~INT -> ~REAL
Figure 25.4 shows:
<A> - <B> <C> - <D> - <E> <F> - <G>
Now suppose the procedures X and Y are defined by:
DEFINE X: <A> ENDDEFN
DEFINE Y: <B> - <C> ENDDEFN
The STATEMENT:
X; Y;
generates an ambiguous phrase consisting of the phrase "<A>" and
the phrase "<B><C>". In contrast:
X; - Y;
generates one phrase, "<A><B><C>". (The semicolons are part of the
atomic STATEMENTs, as:
X;
is the notation for calling procedure X). In general, the normal
~sequential execution of phrase generations "<...>" offers up the
phrases as ambiguous, multiple interpretations sharing the same span
(LEFT and C).
We will see examples of phrase generation from within the semantics of
syntax rules in next chapter.
BOX: What kind of phrase is generated by a sequence of
BOX: STATEMENTs without the dashes?
BOX:
BOX: Can phrase generation be packaged in procedures?
25.5
Two Kinds Of Ambiguity At Once - The Passage Of Ambiguity From One Domain
To The Next
Ambiguities can arise from the syntax grammar and also from the
datatype grammar. Both kinds of ambiguity manifest themselves in the
same way. They result in ambiguous datatype phrases.
25.5.1
Datatype Ambiguities
25.5.1.1
Ambiguities From Coercion
Let's first examine ambiguities that arise from the datatype grammar
alone. For example, the phrase:
1
is turned into the datatype phrase:
~INT
The coercion from INT to REAL:
~INT -> ~REAL
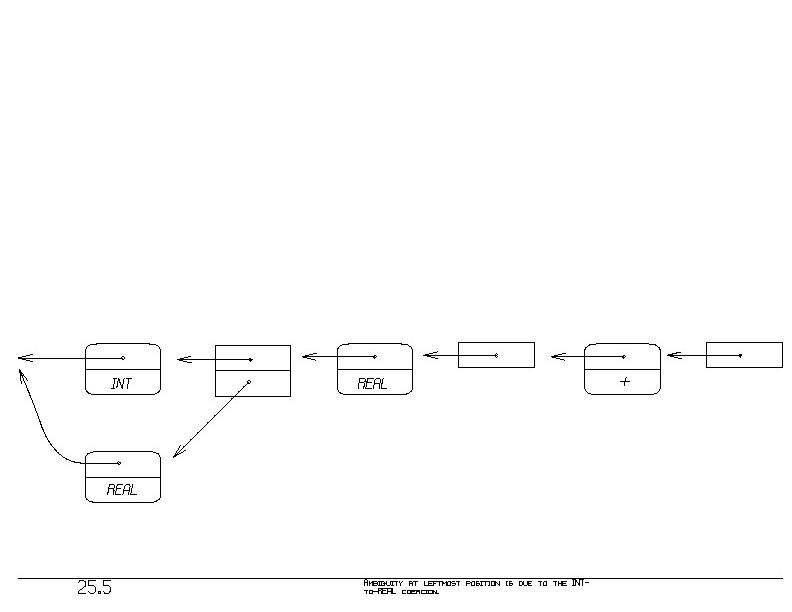 applied to the datatype phrase gives rise to the leftmost two blocks
in figure 25.5. Here we have an ambiguity between INT and REAL: The
"1" is either an INT or REAL.
25.5.1.2
Ambiguities From Polymorphism
Ambiguities may arise from polymorphism as well as coercion. We just
saw one introduced by a coercion.
Here is an example that involves "+"'s polymorphism. Assume we have
only the following rules:
~INT ~INT + -> ~INT
~REAL ~REAL + -> ~REAL
~INT -> ~REAL
The phrase:
1 + 2
which gives rise to the datatype phrase:
~INT ~INT +
can be interpreted as a REAL via ~two means.
applied to the datatype phrase gives rise to the leftmost two blocks
in figure 25.5. Here we have an ambiguity between INT and REAL: The
"1" is either an INT or REAL.
25.5.1.2
Ambiguities From Polymorphism
Ambiguities may arise from polymorphism as well as coercion. We just
saw one introduced by a coercion.
Here is an example that involves "+"'s polymorphism. Assume we have
only the following rules:
~INT ~INT + -> ~INT
~REAL ~REAL + -> ~REAL
~INT -> ~REAL
The phrase:
1 + 2
which gives rise to the datatype phrase:
~INT ~INT +
can be interpreted as a REAL via ~two means.
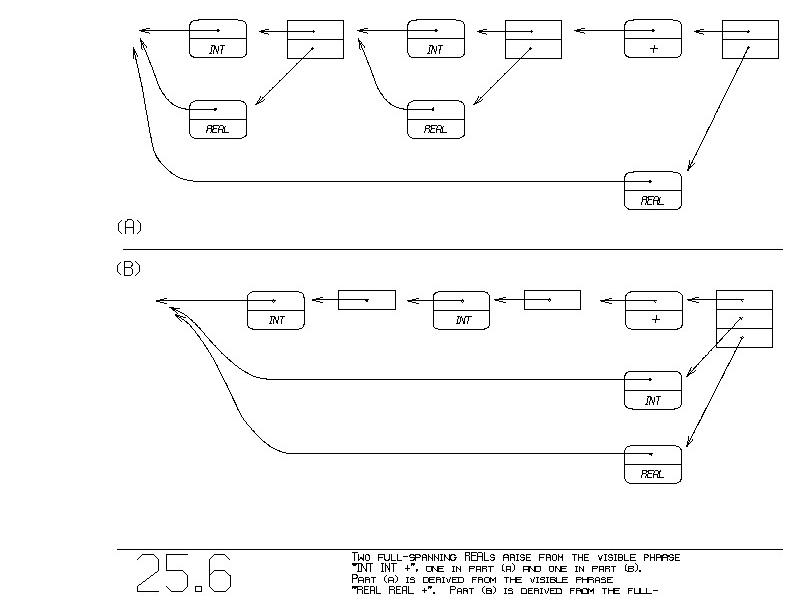 Consider first figure 25.6(a). Each of the two INTs is independently
turned into a REAL, and then the rule:
~REAL ~REAL + -> ~REAL
applies to give an overall REAL interpretation. This is called the
~two-coercion interpretation, because a coercion is applied to each
INT.
Another scenario also occurs. "+" is polymorphic because it will
combine INTs or it will combine REALs. Our second scenario, shown in
figure 25.6(b), has "+" combining the INTs to produce an INT. That
~one combined INT is then turned into a REAL. This is the ~one-
coercion interpretation.
Consider first figure 25.6(a). Each of the two INTs is independently
turned into a REAL, and then the rule:
~REAL ~REAL + -> ~REAL
applies to give an overall REAL interpretation. This is called the
~two-coercion interpretation, because a coercion is applied to each
INT.
Another scenario also occurs. "+" is polymorphic because it will
combine INTs or it will combine REALs. Our second scenario, shown in
figure 25.6(b), has "+" combining the INTs to produce an INT. That
~one combined INT is then turned into a REAL. This is the ~one-
coercion interpretation.
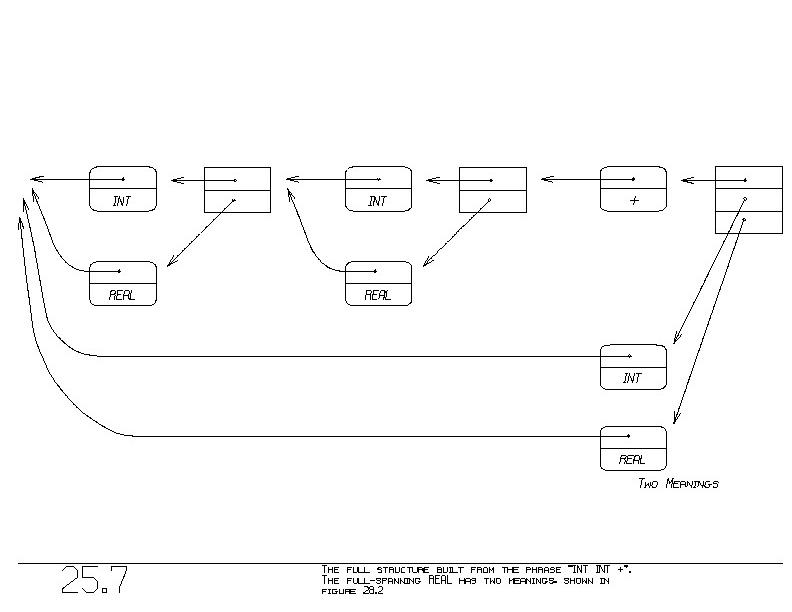 Both these scenarios happen at once, giving rise to figure 25.7. The
full-spanning REAL has two meanings as just discussed. (Figure 28.2
may illustrate these two meanings more clearly).
Later on, when we invoke the semantics of the full-spanning REAL,
both meanings will be considered. A process described in Chapter 28
will choose ultimately the one-coercion solution over the two-
coercion solution.
This concludes our examples of ambiguities within the datatype
language alone.
25.5.2
What Happens To Syntactic Ambiguities?
Recall from Section 15.2 that syntactic ambiguities manifest
themselves as ambiguous semantics. For example, the syntactically
ambiguous phrase:
A + B # C
Both these scenarios happen at once, giving rise to figure 25.7. The
full-spanning REAL has two meanings as just discussed. (Figure 28.2
may illustrate these two meanings more clearly).
Later on, when we invoke the semantics of the full-spanning REAL,
both meanings will be considered. A process described in Chapter 28
will choose ultimately the one-coercion solution over the two-
coercion solution.
This concludes our examples of ambiguities within the datatype
language alone.
25.5.2
What Happens To Syntactic Ambiguities?
Recall from Section 15.2 that syntactic ambiguities manifest
themselves as ambiguous semantics. For example, the syntactically
ambiguous phrase:
A + B # C
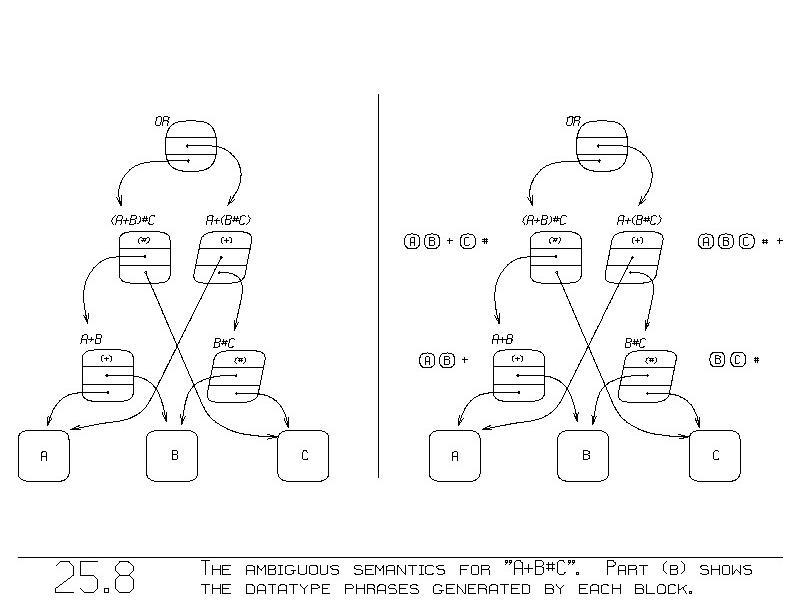 delivers ambiguous semantics, as shown in figure 25.8(a).
Consider the leftmost "+" block in the figure. It is the "+" in "A+B".
As figure 25.8(b) shows, that semantic block generates the reverse
polish phrase:
A B +
where A and B (shown surrounded by circles) denote the ~types of the
variables A and B.
Figure 25.8(b) shows with each semantic block the
reverse polish phrase it generates. For example, the "(A+B)#C" block
generates:
A B + C #
by invoking its sub-block (A+B)'s semantics, which generate the
"A B +". It then invokes its second sub-block (C), which generates
the second part of the phrase, the C. Finally, it appends the "#"
to complete the reverse polish phrase.
Similarly, the other choice, "A+(B#C)", generates the phrase:
A B C # +
~Our ~syntactic ~ambiguity ~gives ~rise ~to ~the ~ambiguous ~datatype
~phrase:
A B + C # ~or A B C # +
Let's go on to see how this ambiguous phrase parses in the datatype
grammar.
25.5.3
Parsing By The Datatype Grammar
delivers ambiguous semantics, as shown in figure 25.8(a).
Consider the leftmost "+" block in the figure. It is the "+" in "A+B".
As figure 25.8(b) shows, that semantic block generates the reverse
polish phrase:
A B +
where A and B (shown surrounded by circles) denote the ~types of the
variables A and B.
Figure 25.8(b) shows with each semantic block the
reverse polish phrase it generates. For example, the "(A+B)#C" block
generates:
A B + C #
by invoking its sub-block (A+B)'s semantics, which generate the
"A B +". It then invokes its second sub-block (C), which generates
the second part of the phrase, the C. Finally, it appends the "#"
to complete the reverse polish phrase.
Similarly, the other choice, "A+(B#C)", generates the phrase:
A B C # +
~Our ~syntactic ~ambiguity ~gives ~rise ~to ~the ~ambiguous ~datatype
~phrase:
A B + C # ~or A B C # +
Let's go on to see how this ambiguous phrase parses in the datatype
grammar.
25.5.3
Parsing By The Datatype Grammar
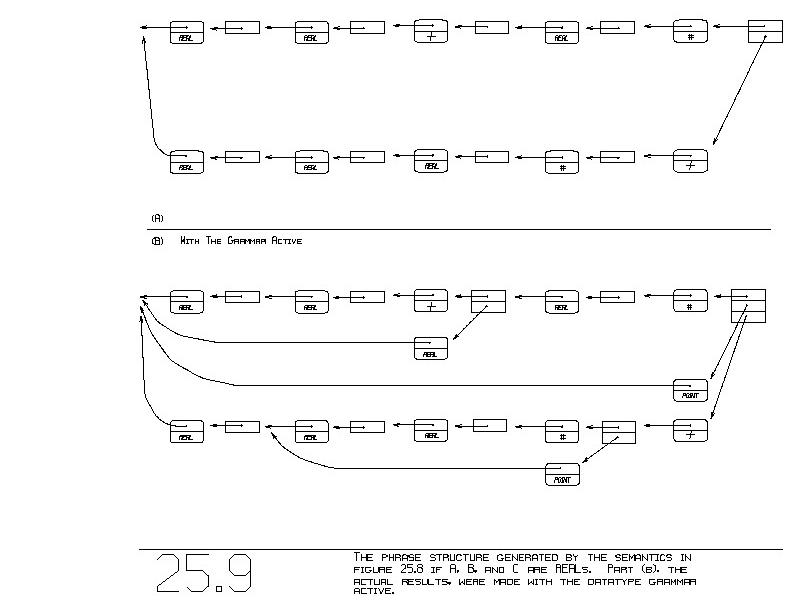 Figure 25.9(a) shows the ambiguous phrase if A, B, and C are all of
type REAL. Part (b) shows what is generated as a by-product of the
grammar.
The datatype rules relevant to this example are:
1) ~REAL ~REAL + -> ~REAL
2) ~POINT ~POINT + -> ~POINT
3) ~REAL ~REAL # -> ~POINT
("+" works on POINTs as well as REALs, and "#" combines two REALs to
form a POINT).
The two phrases making up the ambiguous phrase may or may not
individually parse successfully. For example, suppose the types of A,
B, and C are all REALs. The two phrases appear as:
~REAL ~REAL + ~REAL #
and
~REAL ~REAL ~REAL # +
The first phrase reduces to the following, by rule #1:
~REAL ~REAL #
Rule #3 reduces this successfully to a full-spanning:
~POINT
In contrast, our second phrase can be partially parsed, via rule #3,
to:
~REAL ~POINT +
This final form can be reduced no further. No full-spanning type can
be acquired from this phrase with our rules (barring other coercions).
We've just seen how a syntax ambiguity generates multiple datatype
phrases, some of which might die, being unable to be rendered as a
full-spanning type. Neither, either, or both phrases may succeed.
We've seen one phrase succeed and the other fail.
BOX: If A were of type POINT, what phrase(s) would
BOX: survive?
If the types of A, B, and C were as follows:
A is POINT
B and C are REALs
then the ambiguous phrase would be:
~POINT ~REAL + ~REAL #
~or
~POINT ~REAL ~REAL # +
The latter phrase would be the only survivor (as the "REAL REAL #" goes
to POINT).
If A, B, and C were all POINTs, neither phrase would
survive. If A were itself ambiguous, either a REAL or a POINT, while
B and C were still REALs, ~both phrases would survive.
25.5.4
Under Syntax, What Does The Semantic ~OR Block Do?
In Section 15.2 we characterized the action performed by the ~OR block
as being simply unspecified, a function by the name of F. We are now
in a position to choose a definition for F.
We want the ~OR block to generate an ambiguous phrase, the ambiguous
combination of the phrases generated by each of OR's two components.
We've seen already how to generate ambiguous phrases: Just generate
one phrase and then generate the other phrase. This is two
STATEMENTs executed sequentially, with no dash connecting them. Thus,
we define F via:
DEFINE F( A,B: BASIC_PROCESS ):
<*A*>;
<*B*>;
ENDDEFN
F invokes each of its given components, A, and B, so that each
contributes a phrase, where both phrases share the same span (LEFT and
C).
In figure 25.8(b), the OR-block invokes each of its constituents, and
thus generates the ambiguous phrase:
A B + C # ~or A B C # +
Figure 25.9 shows the generated phrase, if A, B, and C are REALs.
Thus, both syntactic and datatype ambiguities come together in one
formalism. Syntactic ambiguities generate ambiguous datatype phrases,
as also does the datatype grammar on its own. All ambiguities
ultimately reside in the datatype grammar.
BOX: How can ambiguities occur by the datatype grammar
BOX: alone?
BOX:
BOX: How does a syntactic ambiguity manifest itself in the
BOX: datatype language?
BOX:
BOX: What does the OR-block do during the execution of
BOX: syntax's semantics?
25.6
Picking Up The Generated Phrases As A CHOICE_OF_PHRASES
We generate phrases via STATEMENTs, as just shown. Once phrases are
generated, C holds all the phrases as a single CHOICE_OF_PHRASES.
We introduce two notations that turn ~any STATEMENT into a
CHOICE_OF_PHRASES. One of them is:
[-> STATEMENT <-] -> EXPR
(a CHOICE_OF_PHRASES)
This basically executes the STATEMENT and then yields the value
(the generated phrases in C).
This notation translates simply to:
HOLDING C:= NIL;
GIVE
DO ~the_STATEMENT
GIVE C
ENDHOLD
The STATEMENT is executed in a context where C is set to NIL initially.
All phrases generated, which wind up on C, is the value delivered by
this EXPR. (If the STATEMENT performs no phrase generation, then this
EXPR yields NIL).
This new EXPR depends on the variable LEFT. Whatever happens to be
in LEFT upon commencement of this EXPR's execution, will be the left
endpoint for all full-spanning phrases.
Our second notation will be the one we use here almost exclusively:
[> STATEMENT <] -> EXPR
This executes the STATEMENT, and yields ~almost all of
C as its result. It yields only the ~full-spanning phrases in C that
are of ~length ~one. Its translation follows:
HOLDING C:= NIL;
LEFT:= NIL;
GIVE
DO ~the_STATEMENT
GIVE C pruned so as to hold full-spanning unit-
length phrases only
ENDHOLD
Example:
The STATEMENT:
<INT>
generates a CHOICE_OF_PHRASES (on C) that includes at least an
<INT>. If the coercion from INT to REAL is a rule in our
datatype grammar, then C will also contain a <REAL>, sharing
the same span as the <INT>.
Let's enclose this STATEMENT within the "[>...<]":
[> <INT> <]
This EXPR is of type CHOICE_OF_PHRASES, and the value of this
EXPR is the CHOICE_OF_PHRASES that arises on C upon generating
the phrase <INT>. That is, this EXPR is a CHOICE_OF_PHRASES
containing both <INT> and <REAL>.
Example:
While the STATEMENT:
<A>
<B>
<C> - <D>
<E>
~generates the ambiguous phrase in figure 25.3, the EXPR:
[-> <A>
<B>
<C> - <D>
<E> <-]
delivers that generated phrase as a CHOICE_OF_PHRASES, with no
mention made of our variable C.
Our more popular operation with "[>" instead of "[->":
[> <A>
<B>
<C> - <D>
<E> <]
delivers only the full-spanning phrases A, B, and E.
(Conceivably, the "<C>-<D>" phrase, with a grammar active,
could produce other full-spanning phrases, which would then
be included).
Example:
Given the rules:
~INT ~INT plus -> ~INT
~REAL ~REAL plus -> ~REAL
~INT -> ~REAL
the CHOICE_OF_PHRASES delivered by:
[-> <INT> - <INT> - <plus> <-]
is shown in figure 25.7. The one delivered by:
[> <INT> - <INT> - <plus> <]
consists of only two phrases, the full-spanning INT and REAL.
BOX: BOX: What notations do we have that collect up the phrases
BOX: generated by the execution of a STATEMENT?
BOX:
BOX: The expression:
BOX:
BOX: [> <INT> <]
BOX:
BOX: represents what CHOICE_OF_PHRASES, assuming we have
BOX: the INT-to-REAL coercion?
BOX:
BOX: Because:
BOX:
BOX: <INT>
BOX:
BOX: is a STATEMENT, what effect does it have?
25.7
The WANT Quantifier
We now address the last notation required in order to present
a language involving two domains, in our case, syntax and
datatypes.
Suppose we have a CHOICE_OF_PHRASES and we want to find, say, a full-
spanning BOOLean. This need may arise in the implementation of the
syntax rule:
while EXPR ; -> QUANTIFIER
For this quantifier to be meaningful, the EXPR must be of type BOOL.
We can invoke that EXPR's semantics so as to generate all possible
types (phrases) that the EXPR could be interpreted as. Then, using
the notation "[>...<]", we obtain a CHOICE_OF_PHRASES that has all the
full-spanning types of that EXPR. We now are interested in that
full-spanning BOOL within the CHOICE_OF_PHRASES.
Suppose X is the CHOICE_OF_PHRASES. The ~new quantifier:
WANT <BOOL:B> FROM X ;
causes an iteration for each full-spanning BOOL in X. On each of
those iterations, it sets B to the semantics of the matched BOOL.
(According to Section 14.3, there can be at most one full-
spanning BOOL, as duplicate phrases are supressed. This
instance of the WANT quantifier thus causes always zero or one
iterations. It causes zero iterations if there is no full-
spanning BOOL, and one iteration otherwise).
This WANT quantifier translates into our more familiar FOR-quantifier:
FOR P $E X; WITH P.POS = BOOL &
-DEFINED( P.LEFT ) ;
EACH_DO b:= P.SEM ; ;
It looks at all phrase blocks (P) in the CHOICE_OF_PHRASES X, and
causes an iteration for each phrase block whose part-of-speech is BOOL,
and which is full-spanning (the "-defined(P.LEFT)"). It also sets the
matched phrase block's semantics into the variable B (the EACH_DO).
(The "P.SEM" here may be transformed to "<*P.SEM*>" if context
demands that).
The WANT quantifier is supported by the following syntax rule:
want TOKEN from EXPR ; -> QUANTIFER
The TOKEN is just like that admitted on the lefthand side of a rule.
The EXPR must be of type CHOICE_OF_PHRASES.
25.7.1
WANT Quantifier Can Involve Array Parts-Of-Speech
Recall that a TOKEN can be of the form:
< ID [ ID ] : ID >
as in:
<EXPR[I]:X> or <TYPES[T1]:X>
That is, for matching array parts-of-speech, the index variable (the ID
enclosed in "[...]") is also set upon each match.
For example, let's declare an array part-of-speech we will be using for
datatype processing:
POS TYPES[10000] : - ;
We will agree that any datatype is an instance of this TYPES array of
parts-of-speech. Therefore, the quantifier:
WANT <TYPES[T]:S> FROM X ;
may cause more than one iteration. Any part-of-speech that is a
member of the TYPES array of parts-of-speech will be matched, and T
will be set to its index, a different index for each match. We will
see examples of this use of the WANT quantifier in the next chapter.
25.7.2
WANT Can Match A Phrase
In general, the WANT quantifier can specify not only one TOKEN to
match, but a left-to-right sequence of TOKENs to be matched:
want TOKEN TOKEN ... TOKEN from EXPR ; -> QUANTIFIER
For example, consider:
WANT <REAL:a> <INT:b> <plus> FROM X ;
This will cause an iteration for each full-spanning occurence of the
phrase:
<REAL> <INT> <plus>
There will be one match if X is figure 25.7.
25.7.3
WANT Can Recognize Non-Full-Spanning Phrases
Finally, the WANT quantifier can be used even to find non-full-spanning
phrases. The left side of the phrase to match may be augmented via
the syntax:
ID --
as in:
WANT L-- <REAL:a> <INT:b> <plus> FROM X ;
Now all occurences of the phrase:
<REAL> <INT> <plus>
emenating from X will be matched. Upon each match, the new variable L
is set to the left neightbor of the matched phrase.
Now that we can capture the left neighbor of a matched phrase, we can
note an equivalence. For example, the quantifier:
WANT <REAL:a> <INT:b> <plus> FROM X ;
can be written equivalently as:
WANT L1-- <plus> FROM X ;
!!
WANT L2-- <INT:b> FROM L1 ;
!!
WANT <plus> FROM L2 ;
Each of these three quantifiers matches one token of the original
match phrase. Each token is not required to be full-spanning, as the
notation:
ID --
occurs in the first two quantifiers. Notice how the next quantifier
reads the left neighbor set by the previous quantifer (e.g., L1 and
L2).
BOX: Of what use is the WANT quantifier?
BOX:
BOX: How do you specify a WANT quantifier that matches
BOX: phrases of lengths greater than one?
BOX:
BOX: How do you get WANT to match non-full-spanning phrases?
Figure 25.9(a) shows the ambiguous phrase if A, B, and C are all of
type REAL. Part (b) shows what is generated as a by-product of the
grammar.
The datatype rules relevant to this example are:
1) ~REAL ~REAL + -> ~REAL
2) ~POINT ~POINT + -> ~POINT
3) ~REAL ~REAL # -> ~POINT
("+" works on POINTs as well as REALs, and "#" combines two REALs to
form a POINT).
The two phrases making up the ambiguous phrase may or may not
individually parse successfully. For example, suppose the types of A,
B, and C are all REALs. The two phrases appear as:
~REAL ~REAL + ~REAL #
and
~REAL ~REAL ~REAL # +
The first phrase reduces to the following, by rule #1:
~REAL ~REAL #
Rule #3 reduces this successfully to a full-spanning:
~POINT
In contrast, our second phrase can be partially parsed, via rule #3,
to:
~REAL ~POINT +
This final form can be reduced no further. No full-spanning type can
be acquired from this phrase with our rules (barring other coercions).
We've just seen how a syntax ambiguity generates multiple datatype
phrases, some of which might die, being unable to be rendered as a
full-spanning type. Neither, either, or both phrases may succeed.
We've seen one phrase succeed and the other fail.
BOX: If A were of type POINT, what phrase(s) would
BOX: survive?
If the types of A, B, and C were as follows:
A is POINT
B and C are REALs
then the ambiguous phrase would be:
~POINT ~REAL + ~REAL #
~or
~POINT ~REAL ~REAL # +
The latter phrase would be the only survivor (as the "REAL REAL #" goes
to POINT).
If A, B, and C were all POINTs, neither phrase would
survive. If A were itself ambiguous, either a REAL or a POINT, while
B and C were still REALs, ~both phrases would survive.
25.5.4
Under Syntax, What Does The Semantic ~OR Block Do?
In Section 15.2 we characterized the action performed by the ~OR block
as being simply unspecified, a function by the name of F. We are now
in a position to choose a definition for F.
We want the ~OR block to generate an ambiguous phrase, the ambiguous
combination of the phrases generated by each of OR's two components.
We've seen already how to generate ambiguous phrases: Just generate
one phrase and then generate the other phrase. This is two
STATEMENTs executed sequentially, with no dash connecting them. Thus,
we define F via:
DEFINE F( A,B: BASIC_PROCESS ):
<*A*>;
<*B*>;
ENDDEFN
F invokes each of its given components, A, and B, so that each
contributes a phrase, where both phrases share the same span (LEFT and
C).
In figure 25.8(b), the OR-block invokes each of its constituents, and
thus generates the ambiguous phrase:
A B + C # ~or A B C # +
Figure 25.9 shows the generated phrase, if A, B, and C are REALs.
Thus, both syntactic and datatype ambiguities come together in one
formalism. Syntactic ambiguities generate ambiguous datatype phrases,
as also does the datatype grammar on its own. All ambiguities
ultimately reside in the datatype grammar.
BOX: How can ambiguities occur by the datatype grammar
BOX: alone?
BOX:
BOX: How does a syntactic ambiguity manifest itself in the
BOX: datatype language?
BOX:
BOX: What does the OR-block do during the execution of
BOX: syntax's semantics?
25.6
Picking Up The Generated Phrases As A CHOICE_OF_PHRASES
We generate phrases via STATEMENTs, as just shown. Once phrases are
generated, C holds all the phrases as a single CHOICE_OF_PHRASES.
We introduce two notations that turn ~any STATEMENT into a
CHOICE_OF_PHRASES. One of them is:
[-> STATEMENT <-] -> EXPR
(a CHOICE_OF_PHRASES)
This basically executes the STATEMENT and then yields the value
(the generated phrases in C).
This notation translates simply to:
HOLDING C:= NIL;
GIVE
DO ~the_STATEMENT
GIVE C
ENDHOLD
The STATEMENT is executed in a context where C is set to NIL initially.
All phrases generated, which wind up on C, is the value delivered by
this EXPR. (If the STATEMENT performs no phrase generation, then this
EXPR yields NIL).
This new EXPR depends on the variable LEFT. Whatever happens to be
in LEFT upon commencement of this EXPR's execution, will be the left
endpoint for all full-spanning phrases.
Our second notation will be the one we use here almost exclusively:
[> STATEMENT <] -> EXPR
This executes the STATEMENT, and yields ~almost all of
C as its result. It yields only the ~full-spanning phrases in C that
are of ~length ~one. Its translation follows:
HOLDING C:= NIL;
LEFT:= NIL;
GIVE
DO ~the_STATEMENT
GIVE C pruned so as to hold full-spanning unit-
length phrases only
ENDHOLD
Example:
The STATEMENT:
<INT>
generates a CHOICE_OF_PHRASES (on C) that includes at least an
<INT>. If the coercion from INT to REAL is a rule in our
datatype grammar, then C will also contain a <REAL>, sharing
the same span as the <INT>.
Let's enclose this STATEMENT within the "[>...<]":
[> <INT> <]
This EXPR is of type CHOICE_OF_PHRASES, and the value of this
EXPR is the CHOICE_OF_PHRASES that arises on C upon generating
the phrase <INT>. That is, this EXPR is a CHOICE_OF_PHRASES
containing both <INT> and <REAL>.
Example:
While the STATEMENT:
<A>
<B>
<C> - <D>
<E>
~generates the ambiguous phrase in figure 25.3, the EXPR:
[-> <A>
<B>
<C> - <D>
<E> <-]
delivers that generated phrase as a CHOICE_OF_PHRASES, with no
mention made of our variable C.
Our more popular operation with "[>" instead of "[->":
[> <A>
<B>
<C> - <D>
<E> <]
delivers only the full-spanning phrases A, B, and E.
(Conceivably, the "<C>-<D>" phrase, with a grammar active,
could produce other full-spanning phrases, which would then
be included).
Example:
Given the rules:
~INT ~INT plus -> ~INT
~REAL ~REAL plus -> ~REAL
~INT -> ~REAL
the CHOICE_OF_PHRASES delivered by:
[-> <INT> - <INT> - <plus> <-]
is shown in figure 25.7. The one delivered by:
[> <INT> - <INT> - <plus> <]
consists of only two phrases, the full-spanning INT and REAL.
BOX: BOX: What notations do we have that collect up the phrases
BOX: generated by the execution of a STATEMENT?
BOX:
BOX: The expression:
BOX:
BOX: [> <INT> <]
BOX:
BOX: represents what CHOICE_OF_PHRASES, assuming we have
BOX: the INT-to-REAL coercion?
BOX:
BOX: Because:
BOX:
BOX: <INT>
BOX:
BOX: is a STATEMENT, what effect does it have?
25.7
The WANT Quantifier
We now address the last notation required in order to present
a language involving two domains, in our case, syntax and
datatypes.
Suppose we have a CHOICE_OF_PHRASES and we want to find, say, a full-
spanning BOOLean. This need may arise in the implementation of the
syntax rule:
while EXPR ; -> QUANTIFIER
For this quantifier to be meaningful, the EXPR must be of type BOOL.
We can invoke that EXPR's semantics so as to generate all possible
types (phrases) that the EXPR could be interpreted as. Then, using
the notation "[>...<]", we obtain a CHOICE_OF_PHRASES that has all the
full-spanning types of that EXPR. We now are interested in that
full-spanning BOOL within the CHOICE_OF_PHRASES.
Suppose X is the CHOICE_OF_PHRASES. The ~new quantifier:
WANT <BOOL:B> FROM X ;
causes an iteration for each full-spanning BOOL in X. On each of
those iterations, it sets B to the semantics of the matched BOOL.
(According to Section 14.3, there can be at most one full-
spanning BOOL, as duplicate phrases are supressed. This
instance of the WANT quantifier thus causes always zero or one
iterations. It causes zero iterations if there is no full-
spanning BOOL, and one iteration otherwise).
This WANT quantifier translates into our more familiar FOR-quantifier:
FOR P $E X; WITH P.POS = BOOL &
-DEFINED( P.LEFT ) ;
EACH_DO b:= P.SEM ; ;
It looks at all phrase blocks (P) in the CHOICE_OF_PHRASES X, and
causes an iteration for each phrase block whose part-of-speech is BOOL,
and which is full-spanning (the "-defined(P.LEFT)"). It also sets the
matched phrase block's semantics into the variable B (the EACH_DO).
(The "P.SEM" here may be transformed to "<*P.SEM*>" if context
demands that).
The WANT quantifier is supported by the following syntax rule:
want TOKEN from EXPR ; -> QUANTIFER
The TOKEN is just like that admitted on the lefthand side of a rule.
The EXPR must be of type CHOICE_OF_PHRASES.
25.7.1
WANT Quantifier Can Involve Array Parts-Of-Speech
Recall that a TOKEN can be of the form:
< ID [ ID ] : ID >
as in:
<EXPR[I]:X> or <TYPES[T1]:X>
That is, for matching array parts-of-speech, the index variable (the ID
enclosed in "[...]") is also set upon each match.
For example, let's declare an array part-of-speech we will be using for
datatype processing:
POS TYPES[10000] : - ;
We will agree that any datatype is an instance of this TYPES array of
parts-of-speech. Therefore, the quantifier:
WANT <TYPES[T]:S> FROM X ;
may cause more than one iteration. Any part-of-speech that is a
member of the TYPES array of parts-of-speech will be matched, and T
will be set to its index, a different index for each match. We will
see examples of this use of the WANT quantifier in the next chapter.
25.7.2
WANT Can Match A Phrase
In general, the WANT quantifier can specify not only one TOKEN to
match, but a left-to-right sequence of TOKENs to be matched:
want TOKEN TOKEN ... TOKEN from EXPR ; -> QUANTIFIER
For example, consider:
WANT <REAL:a> <INT:b> <plus> FROM X ;
This will cause an iteration for each full-spanning occurence of the
phrase:
<REAL> <INT> <plus>
There will be one match if X is figure 25.7.
25.7.3
WANT Can Recognize Non-Full-Spanning Phrases
Finally, the WANT quantifier can be used even to find non-full-spanning
phrases. The left side of the phrase to match may be augmented via
the syntax:
ID --
as in:
WANT L-- <REAL:a> <INT:b> <plus> FROM X ;
Now all occurences of the phrase:
<REAL> <INT> <plus>
emenating from X will be matched. Upon each match, the new variable L
is set to the left neightbor of the matched phrase.
Now that we can capture the left neighbor of a matched phrase, we can
note an equivalence. For example, the quantifier:
WANT <REAL:a> <INT:b> <plus> FROM X ;
can be written equivalently as:
WANT L1-- <plus> FROM X ;
!!
WANT L2-- <INT:b> FROM L1 ;
!!
WANT <plus> FROM L2 ;
Each of these three quantifiers matches one token of the original
match phrase. Each token is not required to be full-spanning, as the
notation:
ID --
occurs in the first two quantifiers. Notice how the next quantifier
reads the left neighbor set by the previous quantifer (e.g., L1 and
L2).
BOX: Of what use is the WANT quantifier?
BOX:
BOX: How do you specify a WANT quantifier that matches
BOX: phrases of lengths greater than one?
BOX:
BOX: How do you get WANT to match non-full-spanning phrases?
 LEFT, a CHOICE_OF_PHRASES, denotes the left neighbor for a generated
phrase. The variable C, also a CHOICE_OF_PHRASES, denotes the
righthand edge for the generated phrase. Figure 25.1 illustrates this.
The "<...>" notation, the GIVE, reads these two variables implicitly.
Thus, the values in those two variables are important whenever we
see a "<...>".
How are these variables set?
25.4.1
A Rule's Want-Phrase Sets LEFT
LEFT is set upon matching a want-phrase. Recall that a rule:
<POS(1)> <POS(2)> ... <POS(k)> -> some_action
is turned into a program via the following (from the end of Section
12.3.3). P is the PHRASE block passed to GIVE (and the grammar):
P(k):= P ;
IF P(k).POS = POS(k) THEN
FOR P(k-1) $E P(k).LEFT; WITH P(k-1).POS = POS(k-1) ;
!!
...
!!
FOR P(1) $E P(2).LEFT; WITH P(1).POS = POS(1);
DO
~LEFT:= ~P(1).LEFT;
some_action
END
FI
The "some_action" is executed in a context where LEFT points to the
matched phrase's lefthand neighbor.
---------------- Parentheses in previous paragraph around "1", "2"
---------------- "k", and "k-1" mean subscripting! ---------------------
The action is usually:
GIVE( [ LEFT: LEFT POS: the_righthand_part_of_speech
SEM: //...\\ ] );
This is so if the righthand side of the rule is of the form:
< ID : STATEMENT >
This action now executes in the context where LEFT is the lefthand
neighbor of the matched want-phrase. As always, C holds the rightmost
PHRASE block of the matched phrase (Section 12.3.1).
GIVE will put the newly generated phrase's rightmost block also onto
C. Thus, the newly generated unit-length phrase ~shares ~the ~same
~span (LEFT and C) with the matched want-phrase.
BOX: What do the variables LEFT and C signify?
BOX:
BOX: Why does the generated give-phrase (in a context-free
BOX: rule) share the same span with the matched occurence
BOX: of the rule's want-phrase?
25.4.2
Phrases Of Length Greater Than One
The treatment of the global variables LEFT and C that we saw with
general rewrite rules (Section 12.5) and the taking of user input
(Section 12.4), are now rendered implicit with a new notation.
25.4.2.1
Brief Notation For Setting LEFT and C
STATEMENTs may be combined in a way other than sequential execution.
The "-" may be used to combine STATEMENTs, as supported by the rule:
STATEMENT - STATEMENT - ... - STATEMENT -> STATEMENT
The dashes deal with the variables LEFT and C. LEFT and C are set
up especially for each of the individual STATEMENTs.
This dash notation is meant to be used for generating phrases of length
greater than one. For example:
<POS(1)> - <POS(2)>
combines with a dash the two STATEMENTS:
<POS(1)> and <POS(2)>
This forms a phrase of length two.
---------------- Parentheses in previous paragraph mean subscripting! ---
A general rewrite rule is actually written as:
<POS(1)> ... <POS(k)> -> <GIVE_POS(1)> - ... - <GIVE_POS(n)>
where dashes separate the phrase elements on the righthand side of
the rule. This is our official notation for general rewrite rules
(rather than the dashless notation used in Section 1.3).
---------------- Parentheses in previous paragraph around "1" and "k"
---------------- mean subscripting! -----------------------
How is the rule:
STATEMENT - STATEMENT - ... - STATEMENT -> STATEMENT
implemented? It translates (see Section 12.5) to the following.
(Back there, each STATEMENT was a call to GIVE):
HOLDING LEFT; "(Preserve LEFT so that it looks like we never
modified it)"
DO
RIGHTHAND:= C; "Remember present C, for our final
STATEMENT"
C:= NIL; ~STATEMENT(1)
LEFT:= C; C:= NIL; ~STATEMENT(2)
LEFT:= C; C:= NIL; ~STATEMENT(3)
...
LEFT:= C; C:= NIL; ~STATEMENT(n-1)
LEFT:= C; C:= RIGHTHAND; ~STATEMENT(n)
ENDHOLD
Assuming that each of the STATEMENTs is of the form:
< ID : STATEMENT >
then the overall effect is to generate the entire phrase (connected
by dashes) with LEFT as its left neighbor, where the rightmost phrase
block is appended onto C.
---------------- Parentheses in previous paragraph around "1", "2"
---------------- "3", and "n" and "n-1"" mean subscripting! ------------
That is, where we wrote:
< ID : STATEMENT >
to generate a phrase of length one, spanning from LEFT to C, we can now
write:
<ID : STATEMENT> - <ID : STATEMENT> - ... - <ID : STATEMENT>
to generate a phrase of length greater than one, also spanning from
LEFT to C.
NOTE: STATEMENTs connected with dashes bind together ~before
STATEMENTs separated by nothing (our usual way for putting
STATEMENTs together). Thus,
<A> <B> <C> - <D> <E>
groups as:
<A> <B> (<C> - <D>) <E>
Also:
<A> - <B> <C> - <D> - <E> <F> - <G>
groups as:
(<A> - <B>) (<C> - <D> - <E>) (<F> - <G>)
BOX: BOX: How do you combine STATEMENTs so as to generate a
BOX: phrase of length greater than one?
BOX:
BOX: Is the implementation identical to how we generate
BOX: the give-phrase of a general rewrite rule?
25.4.3
Ambiguous Phrase Generation: Phrase Generation Without The Dashes
LEFT, a CHOICE_OF_PHRASES, denotes the left neighbor for a generated
phrase. The variable C, also a CHOICE_OF_PHRASES, denotes the
righthand edge for the generated phrase. Figure 25.1 illustrates this.
The "<...>" notation, the GIVE, reads these two variables implicitly.
Thus, the values in those two variables are important whenever we
see a "<...>".
How are these variables set?
25.4.1
A Rule's Want-Phrase Sets LEFT
LEFT is set upon matching a want-phrase. Recall that a rule:
<POS(1)> <POS(2)> ... <POS(k)> -> some_action
is turned into a program via the following (from the end of Section
12.3.3). P is the PHRASE block passed to GIVE (and the grammar):
P(k):= P ;
IF P(k).POS = POS(k) THEN
FOR P(k-1) $E P(k).LEFT; WITH P(k-1).POS = POS(k-1) ;
!!
...
!!
FOR P(1) $E P(2).LEFT; WITH P(1).POS = POS(1);
DO
~LEFT:= ~P(1).LEFT;
some_action
END
FI
The "some_action" is executed in a context where LEFT points to the
matched phrase's lefthand neighbor.
---------------- Parentheses in previous paragraph around "1", "2"
---------------- "k", and "k-1" mean subscripting! ---------------------
The action is usually:
GIVE( [ LEFT: LEFT POS: the_righthand_part_of_speech
SEM: //...\\ ] );
This is so if the righthand side of the rule is of the form:
< ID : STATEMENT >
This action now executes in the context where LEFT is the lefthand
neighbor of the matched want-phrase. As always, C holds the rightmost
PHRASE block of the matched phrase (Section 12.3.1).
GIVE will put the newly generated phrase's rightmost block also onto
C. Thus, the newly generated unit-length phrase ~shares ~the ~same
~span (LEFT and C) with the matched want-phrase.
BOX: What do the variables LEFT and C signify?
BOX:
BOX: Why does the generated give-phrase (in a context-free
BOX: rule) share the same span with the matched occurence
BOX: of the rule's want-phrase?
25.4.2
Phrases Of Length Greater Than One
The treatment of the global variables LEFT and C that we saw with
general rewrite rules (Section 12.5) and the taking of user input
(Section 12.4), are now rendered implicit with a new notation.
25.4.2.1
Brief Notation For Setting LEFT and C
STATEMENTs may be combined in a way other than sequential execution.
The "-" may be used to combine STATEMENTs, as supported by the rule:
STATEMENT - STATEMENT - ... - STATEMENT -> STATEMENT
The dashes deal with the variables LEFT and C. LEFT and C are set
up especially for each of the individual STATEMENTs.
This dash notation is meant to be used for generating phrases of length
greater than one. For example:
<POS(1)> - <POS(2)>
combines with a dash the two STATEMENTS:
<POS(1)> and <POS(2)>
This forms a phrase of length two.
---------------- Parentheses in previous paragraph mean subscripting! ---
A general rewrite rule is actually written as:
<POS(1)> ... <POS(k)> -> <GIVE_POS(1)> - ... - <GIVE_POS(n)>
where dashes separate the phrase elements on the righthand side of
the rule. This is our official notation for general rewrite rules
(rather than the dashless notation used in Section 1.3).
---------------- Parentheses in previous paragraph around "1" and "k"
---------------- mean subscripting! -----------------------
How is the rule:
STATEMENT - STATEMENT - ... - STATEMENT -> STATEMENT
implemented? It translates (see Section 12.5) to the following.
(Back there, each STATEMENT was a call to GIVE):
HOLDING LEFT; "(Preserve LEFT so that it looks like we never
modified it)"
DO
RIGHTHAND:= C; "Remember present C, for our final
STATEMENT"
C:= NIL; ~STATEMENT(1)
LEFT:= C; C:= NIL; ~STATEMENT(2)
LEFT:= C; C:= NIL; ~STATEMENT(3)
...
LEFT:= C; C:= NIL; ~STATEMENT(n-1)
LEFT:= C; C:= RIGHTHAND; ~STATEMENT(n)
ENDHOLD
Assuming that each of the STATEMENTs is of the form:
< ID : STATEMENT >
then the overall effect is to generate the entire phrase (connected
by dashes) with LEFT as its left neighbor, where the rightmost phrase
block is appended onto C.
---------------- Parentheses in previous paragraph around "1", "2"
---------------- "3", and "n" and "n-1"" mean subscripting! ------------
That is, where we wrote:
< ID : STATEMENT >
to generate a phrase of length one, spanning from LEFT to C, we can now
write:
<ID : STATEMENT> - <ID : STATEMENT> - ... - <ID : STATEMENT>
to generate a phrase of length greater than one, also spanning from
LEFT to C.
NOTE: STATEMENTs connected with dashes bind together ~before
STATEMENTs separated by nothing (our usual way for putting
STATEMENTs together). Thus,
<A> <B> <C> - <D> <E>
groups as:
<A> <B> (<C> - <D>) <E>
Also:
<A> - <B> <C> - <D> - <E> <F> - <G>
groups as:
(<A> - <B>) (<C> - <D> - <E>) (<F> - <G>)
BOX: BOX: How do you combine STATEMENTs so as to generate a
BOX: phrase of length greater than one?
BOX:
BOX: Is the implementation identical to how we generate
BOX: the give-phrase of a general rewrite rule?
25.4.3
Ambiguous Phrase Generation: Phrase Generation Without The Dashes
 Figure 25.2(a) shows what is built when you execute the statement:
<X> - <Y> - <Z>
Figure 25.2(b) shows what:
<X> <Y> <Z>
generates. With the dashes, we get a left-to-right phrase.
Without the dashes, the three short phrases become one ambiguous
phrase. They all become members of the same CHOICE_OF_PHRASES.
This is natural because the dashless STATEMENT calls GIVE once per
short phrase, without touching C nor LEFT. GIVE puts all its given
phrases onto the same CHOICE_OF_PHRASES, C.
Figure 25.2(a) shows what is built when you execute the statement:
<X> - <Y> - <Z>
Figure 25.2(b) shows what:
<X> <Y> <Z>
generates. With the dashes, we get a left-to-right phrase.
Without the dashes, the three short phrases become one ambiguous
phrase. They all become members of the same CHOICE_OF_PHRASES.
This is natural because the dashless STATEMENT calls GIVE once per
short phrase, without touching C nor LEFT. GIVE puts all its given
phrases onto the same CHOICE_OF_PHRASES, C.
 For another example, figure 25.3 shows what is built upon the execution
of:
<A> <B> <C> - <D> <E>
For another example, figure 25.3 shows what is built upon the execution
of:
<A> <B> <C> - <D> <E>
 Figure 25.4 shows:
<A> - <B> <C> - <D> - <E> <F> - <G>
Now suppose the procedures X and Y are defined by:
DEFINE X: <A> ENDDEFN
DEFINE Y: <B> - <C> ENDDEFN
The STATEMENT:
X; Y;
generates an ambiguous phrase consisting of the phrase "<A>" and
the phrase "<B><C>". In contrast:
X; - Y;
generates one phrase, "<A><B><C>". (The semicolons are part of the
atomic STATEMENTs, as:
X;
is the notation for calling procedure X). In general, the normal
~sequential execution of phrase generations "<...>" offers up the
phrases as ambiguous, multiple interpretations sharing the same span
(LEFT and C).
We will see examples of phrase generation from within the semantics of
syntax rules in next chapter.
BOX: What kind of phrase is generated by a sequence of
BOX: STATEMENTs without the dashes?
BOX:
BOX: Can phrase generation be packaged in procedures?
25.5
Two Kinds Of Ambiguity At Once - The Passage Of Ambiguity From One Domain
To The Next
Ambiguities can arise from the syntax grammar and also from the
datatype grammar. Both kinds of ambiguity manifest themselves in the
same way. They result in ambiguous datatype phrases.
25.5.1
Datatype Ambiguities
25.5.1.1
Ambiguities From Coercion
Let's first examine ambiguities that arise from the datatype grammar
alone. For example, the phrase:
1
is turned into the datatype phrase:
~INT
The coercion from INT to REAL:
~INT -> ~REAL
Figure 25.4 shows:
<A> - <B> <C> - <D> - <E> <F> - <G>
Now suppose the procedures X and Y are defined by:
DEFINE X: <A> ENDDEFN
DEFINE Y: <B> - <C> ENDDEFN
The STATEMENT:
X; Y;
generates an ambiguous phrase consisting of the phrase "<A>" and
the phrase "<B><C>". In contrast:
X; - Y;
generates one phrase, "<A><B><C>". (The semicolons are part of the
atomic STATEMENTs, as:
X;
is the notation for calling procedure X). In general, the normal
~sequential execution of phrase generations "<...>" offers up the
phrases as ambiguous, multiple interpretations sharing the same span
(LEFT and C).
We will see examples of phrase generation from within the semantics of
syntax rules in next chapter.
BOX: What kind of phrase is generated by a sequence of
BOX: STATEMENTs without the dashes?
BOX:
BOX: Can phrase generation be packaged in procedures?
25.5
Two Kinds Of Ambiguity At Once - The Passage Of Ambiguity From One Domain
To The Next
Ambiguities can arise from the syntax grammar and also from the
datatype grammar. Both kinds of ambiguity manifest themselves in the
same way. They result in ambiguous datatype phrases.
25.5.1
Datatype Ambiguities
25.5.1.1
Ambiguities From Coercion
Let's first examine ambiguities that arise from the datatype grammar
alone. For example, the phrase:
1
is turned into the datatype phrase:
~INT
The coercion from INT to REAL:
~INT -> ~REAL
 applied to the datatype phrase gives rise to the leftmost two blocks
in figure 25.5. Here we have an ambiguity between INT and REAL: The
"1" is either an INT or REAL.
25.5.1.2
Ambiguities From Polymorphism
Ambiguities may arise from polymorphism as well as coercion. We just
saw one introduced by a coercion.
Here is an example that involves "+"'s polymorphism. Assume we have
only the following rules:
~INT ~INT + -> ~INT
~REAL ~REAL + -> ~REAL
~INT -> ~REAL
The phrase:
1 + 2
which gives rise to the datatype phrase:
~INT ~INT +
can be interpreted as a REAL via ~two means.
applied to the datatype phrase gives rise to the leftmost two blocks
in figure 25.5. Here we have an ambiguity between INT and REAL: The
"1" is either an INT or REAL.
25.5.1.2
Ambiguities From Polymorphism
Ambiguities may arise from polymorphism as well as coercion. We just
saw one introduced by a coercion.
Here is an example that involves "+"'s polymorphism. Assume we have
only the following rules:
~INT ~INT + -> ~INT
~REAL ~REAL + -> ~REAL
~INT -> ~REAL
The phrase:
1 + 2
which gives rise to the datatype phrase:
~INT ~INT +
can be interpreted as a REAL via ~two means.
 Consider first figure 25.6(a). Each of the two INTs is independently
turned into a REAL, and then the rule:
~REAL ~REAL + -> ~REAL
applies to give an overall REAL interpretation. This is called the
~two-coercion interpretation, because a coercion is applied to each
INT.
Another scenario also occurs. "+" is polymorphic because it will
combine INTs or it will combine REALs. Our second scenario, shown in
figure 25.6(b), has "+" combining the INTs to produce an INT. That
~one combined INT is then turned into a REAL. This is the ~one-
coercion interpretation.
Consider first figure 25.6(a). Each of the two INTs is independently
turned into a REAL, and then the rule:
~REAL ~REAL + -> ~REAL
applies to give an overall REAL interpretation. This is called the
~two-coercion interpretation, because a coercion is applied to each
INT.
Another scenario also occurs. "+" is polymorphic because it will
combine INTs or it will combine REALs. Our second scenario, shown in
figure 25.6(b), has "+" combining the INTs to produce an INT. That
~one combined INT is then turned into a REAL. This is the ~one-
coercion interpretation.
 Both these scenarios happen at once, giving rise to figure 25.7. The
full-spanning REAL has two meanings as just discussed. (Figure 28.2
may illustrate these two meanings more clearly).
Later on, when we invoke the semantics of the full-spanning REAL,
both meanings will be considered. A process described in Chapter 28
will choose ultimately the one-coercion solution over the two-
coercion solution.
This concludes our examples of ambiguities within the datatype
language alone.
25.5.2
What Happens To Syntactic Ambiguities?
Recall from Section 15.2 that syntactic ambiguities manifest
themselves as ambiguous semantics. For example, the syntactically
ambiguous phrase:
A + B # C
Both these scenarios happen at once, giving rise to figure 25.7. The
full-spanning REAL has two meanings as just discussed. (Figure 28.2
may illustrate these two meanings more clearly).
Later on, when we invoke the semantics of the full-spanning REAL,
both meanings will be considered. A process described in Chapter 28
will choose ultimately the one-coercion solution over the two-
coercion solution.
This concludes our examples of ambiguities within the datatype
language alone.
25.5.2
What Happens To Syntactic Ambiguities?
Recall from Section 15.2 that syntactic ambiguities manifest
themselves as ambiguous semantics. For example, the syntactically
ambiguous phrase:
A + B # C
 delivers ambiguous semantics, as shown in figure 25.8(a).
Consider the leftmost "+" block in the figure. It is the "+" in "A+B".
As figure 25.8(b) shows, that semantic block generates the reverse
polish phrase:
A B +
where A and B (shown surrounded by circles) denote the ~types of the
variables A and B.
Figure 25.8(b) shows with each semantic block the
reverse polish phrase it generates. For example, the "(A+B)#C" block
generates:
A B + C #
by invoking its sub-block (A+B)'s semantics, which generate the
"A B +". It then invokes its second sub-block (C), which generates
the second part of the phrase, the C. Finally, it appends the "#"
to complete the reverse polish phrase.
Similarly, the other choice, "A+(B#C)", generates the phrase:
A B C # +
~Our ~syntactic ~ambiguity ~gives ~rise ~to ~the ~ambiguous ~datatype
~phrase:
A B + C # ~or A B C # +
Let's go on to see how this ambiguous phrase parses in the datatype
grammar.
25.5.3
Parsing By The Datatype Grammar
delivers ambiguous semantics, as shown in figure 25.8(a).
Consider the leftmost "+" block in the figure. It is the "+" in "A+B".
As figure 25.8(b) shows, that semantic block generates the reverse
polish phrase:
A B +
where A and B (shown surrounded by circles) denote the ~types of the
variables A and B.
Figure 25.8(b) shows with each semantic block the
reverse polish phrase it generates. For example, the "(A+B)#C" block
generates:
A B + C #
by invoking its sub-block (A+B)'s semantics, which generate the
"A B +". It then invokes its second sub-block (C), which generates
the second part of the phrase, the C. Finally, it appends the "#"
to complete the reverse polish phrase.
Similarly, the other choice, "A+(B#C)", generates the phrase:
A B C # +
~Our ~syntactic ~ambiguity ~gives ~rise ~to ~the ~ambiguous ~datatype
~phrase:
A B + C # ~or A B C # +
Let's go on to see how this ambiguous phrase parses in the datatype
grammar.
25.5.3
Parsing By The Datatype Grammar
 Figure 25.9(a) shows the ambiguous phrase if A, B, and C are all of
type REAL. Part (b) shows what is generated as a by-product of the
grammar.
The datatype rules relevant to this example are:
1) ~REAL ~REAL + -> ~REAL
2) ~POINT ~POINT + -> ~POINT
3) ~REAL ~REAL # -> ~POINT
("+" works on POINTs as well as REALs, and "#" combines two REALs to
form a POINT).
The two phrases making up the ambiguous phrase may or may not
individually parse successfully. For example, suppose the types of A,
B, and C are all REALs. The two phrases appear as:
~REAL ~REAL + ~REAL #
and
~REAL ~REAL ~REAL # +
The first phrase reduces to the following, by rule #1:
~REAL ~REAL #
Rule #3 reduces this successfully to a full-spanning:
~POINT
In contrast, our second phrase can be partially parsed, via rule #3,
to:
~REAL ~POINT +
This final form can be reduced no further. No full-spanning type can
be acquired from this phrase with our rules (barring other coercions).
We've just seen how a syntax ambiguity generates multiple datatype
phrases, some of which might die, being unable to be rendered as a
full-spanning type. Neither, either, or both phrases may succeed.
We've seen one phrase succeed and the other fail.
BOX: If A were of type POINT, what phrase(s) would
BOX: survive?
If the types of A, B, and C were as follows:
A is POINT
B and C are REALs
then the ambiguous phrase would be:
~POINT ~REAL + ~REAL #
~or
~POINT ~REAL ~REAL # +
The latter phrase would be the only survivor (as the "REAL REAL #" goes
to POINT).
If A, B, and C were all POINTs, neither phrase would
survive. If A were itself ambiguous, either a REAL or a POINT, while
B and C were still REALs, ~both phrases would survive.
25.5.4
Under Syntax, What Does The Semantic ~OR Block Do?
In Section 15.2 we characterized the action performed by the ~OR block
as being simply unspecified, a function by the name of F. We are now
in a position to choose a definition for F.
We want the ~OR block to generate an ambiguous phrase, the ambiguous
combination of the phrases generated by each of OR's two components.
We've seen already how to generate ambiguous phrases: Just generate
one phrase and then generate the other phrase. This is two
STATEMENTs executed sequentially, with no dash connecting them. Thus,
we define F via:
DEFINE F( A,B: BASIC_PROCESS ):
<*A*>;
<*B*>;
ENDDEFN
F invokes each of its given components, A, and B, so that each
contributes a phrase, where both phrases share the same span (LEFT and
C).
In figure 25.8(b), the OR-block invokes each of its constituents, and
thus generates the ambiguous phrase:
A B + C # ~or A B C # +
Figure 25.9 shows the generated phrase, if A, B, and C are REALs.
Thus, both syntactic and datatype ambiguities come together in one
formalism. Syntactic ambiguities generate ambiguous datatype phrases,
as also does the datatype grammar on its own. All ambiguities
ultimately reside in the datatype grammar.
BOX: How can ambiguities occur by the datatype grammar
BOX: alone?
BOX:
BOX: How does a syntactic ambiguity manifest itself in the
BOX: datatype language?
BOX:
BOX: What does the OR-block do during the execution of
BOX: syntax's semantics?
25.6
Picking Up The Generated Phrases As A CHOICE_OF_PHRASES
We generate phrases via STATEMENTs, as just shown. Once phrases are
generated, C holds all the phrases as a single CHOICE_OF_PHRASES.
We introduce two notations that turn ~any STATEMENT into a
CHOICE_OF_PHRASES. One of them is:
[-> STATEMENT <-] -> EXPR
(a CHOICE_OF_PHRASES)
This basically executes the STATEMENT and then yields the value
(the generated phrases in C).
This notation translates simply to:
HOLDING C:= NIL;
GIVE
DO ~the_STATEMENT
GIVE C
ENDHOLD
The STATEMENT is executed in a context where C is set to NIL initially.
All phrases generated, which wind up on C, is the value delivered by
this EXPR. (If the STATEMENT performs no phrase generation, then this
EXPR yields NIL).
This new EXPR depends on the variable LEFT. Whatever happens to be
in LEFT upon commencement of this EXPR's execution, will be the left
endpoint for all full-spanning phrases.
Our second notation will be the one we use here almost exclusively:
[> STATEMENT <] -> EXPR
This executes the STATEMENT, and yields ~almost all of
C as its result. It yields only the ~full-spanning phrases in C that
are of ~length ~one. Its translation follows:
HOLDING C:= NIL;
LEFT:= NIL;
GIVE
DO ~the_STATEMENT
GIVE C pruned so as to hold full-spanning unit-
length phrases only
ENDHOLD
Example:
The STATEMENT:
<INT>
generates a CHOICE_OF_PHRASES (on C) that includes at least an
<INT>. If the coercion from INT to REAL is a rule in our
datatype grammar, then C will also contain a <REAL>, sharing
the same span as the <INT>.
Let's enclose this STATEMENT within the "[>...<]":
[> <INT> <]
This EXPR is of type CHOICE_OF_PHRASES, and the value of this
EXPR is the CHOICE_OF_PHRASES that arises on C upon generating
the phrase <INT>. That is, this EXPR is a CHOICE_OF_PHRASES
containing both <INT> and <REAL>.
Example:
While the STATEMENT:
<A>
<B>
<C> - <D>
<E>
~generates the ambiguous phrase in figure 25.3, the EXPR:
[-> <A>
<B>
<C> - <D>
<E> <-]
delivers that generated phrase as a CHOICE_OF_PHRASES, with no
mention made of our variable C.
Our more popular operation with "[>" instead of "[->":
[> <A>
<B>
<C> - <D>
<E> <]
delivers only the full-spanning phrases A, B, and E.
(Conceivably, the "<C>-<D>" phrase, with a grammar active,
could produce other full-spanning phrases, which would then
be included).
Example:
Given the rules:
~INT ~INT plus -> ~INT
~REAL ~REAL plus -> ~REAL
~INT -> ~REAL
the CHOICE_OF_PHRASES delivered by:
[-> <INT> - <INT> - <plus> <-]
is shown in figure 25.7. The one delivered by:
[> <INT> - <INT> - <plus> <]
consists of only two phrases, the full-spanning INT and REAL.
BOX: BOX: What notations do we have that collect up the phrases
BOX: generated by the execution of a STATEMENT?
BOX:
BOX: The expression:
BOX:
BOX: [> <INT> <]
BOX:
BOX: represents what CHOICE_OF_PHRASES, assuming we have
BOX: the INT-to-REAL coercion?
BOX:
BOX: Because:
BOX:
BOX: <INT>
BOX:
BOX: is a STATEMENT, what effect does it have?
25.7
The WANT Quantifier
We now address the last notation required in order to present
a language involving two domains, in our case, syntax and
datatypes.
Suppose we have a CHOICE_OF_PHRASES and we want to find, say, a full-
spanning BOOLean. This need may arise in the implementation of the
syntax rule:
while EXPR ; -> QUANTIFIER
For this quantifier to be meaningful, the EXPR must be of type BOOL.
We can invoke that EXPR's semantics so as to generate all possible
types (phrases) that the EXPR could be interpreted as. Then, using
the notation "[>...<]", we obtain a CHOICE_OF_PHRASES that has all the
full-spanning types of that EXPR. We now are interested in that
full-spanning BOOL within the CHOICE_OF_PHRASES.
Suppose X is the CHOICE_OF_PHRASES. The ~new quantifier:
WANT <BOOL:B> FROM X ;
causes an iteration for each full-spanning BOOL in X. On each of
those iterations, it sets B to the semantics of the matched BOOL.
(According to Section 14.3, there can be at most one full-
spanning BOOL, as duplicate phrases are supressed. This
instance of the WANT quantifier thus causes always zero or one
iterations. It causes zero iterations if there is no full-
spanning BOOL, and one iteration otherwise).
This WANT quantifier translates into our more familiar FOR-quantifier:
FOR P $E X; WITH P.POS = BOOL &
-DEFINED( P.LEFT ) ;
EACH_DO b:= P.SEM ; ;
It looks at all phrase blocks (P) in the CHOICE_OF_PHRASES X, and
causes an iteration for each phrase block whose part-of-speech is BOOL,
and which is full-spanning (the "-defined(P.LEFT)"). It also sets the
matched phrase block's semantics into the variable B (the EACH_DO).
(The "P.SEM" here may be transformed to "<*P.SEM*>" if context
demands that).
The WANT quantifier is supported by the following syntax rule:
want TOKEN from EXPR ; -> QUANTIFER
The TOKEN is just like that admitted on the lefthand side of a rule.
The EXPR must be of type CHOICE_OF_PHRASES.
25.7.1
WANT Quantifier Can Involve Array Parts-Of-Speech
Recall that a TOKEN can be of the form:
< ID [ ID ] : ID >
as in:
<EXPR[I]:X> or <TYPES[T1]:X>
That is, for matching array parts-of-speech, the index variable (the ID
enclosed in "[...]") is also set upon each match.
For example, let's declare an array part-of-speech we will be using for
datatype processing:
POS TYPES[10000] : - ;
We will agree that any datatype is an instance of this TYPES array of
parts-of-speech. Therefore, the quantifier:
WANT <TYPES[T]:S> FROM X ;
may cause more than one iteration. Any part-of-speech that is a
member of the TYPES array of parts-of-speech will be matched, and T
will be set to its index, a different index for each match. We will
see examples of this use of the WANT quantifier in the next chapter.
25.7.2
WANT Can Match A Phrase
In general, the WANT quantifier can specify not only one TOKEN to
match, but a left-to-right sequence of TOKENs to be matched:
want TOKEN TOKEN ... TOKEN from EXPR ; -> QUANTIFIER
For example, consider:
WANT <REAL:a> <INT:b> <plus> FROM X ;
This will cause an iteration for each full-spanning occurence of the
phrase:
<REAL> <INT> <plus>
There will be one match if X is figure 25.7.
25.7.3
WANT Can Recognize Non-Full-Spanning Phrases
Finally, the WANT quantifier can be used even to find non-full-spanning
phrases. The left side of the phrase to match may be augmented via
the syntax:
ID --
as in:
WANT L-- <REAL:a> <INT:b> <plus> FROM X ;
Now all occurences of the phrase:
<REAL> <INT> <plus>
emenating from X will be matched. Upon each match, the new variable L
is set to the left neightbor of the matched phrase.
Now that we can capture the left neighbor of a matched phrase, we can
note an equivalence. For example, the quantifier:
WANT <REAL:a> <INT:b> <plus> FROM X ;
can be written equivalently as:
WANT L1-- <plus> FROM X ;
!!
WANT L2-- <INT:b> FROM L1 ;
!!
WANT <plus> FROM L2 ;
Each of these three quantifiers matches one token of the original
match phrase. Each token is not required to be full-spanning, as the
notation:
ID --
occurs in the first two quantifiers. Notice how the next quantifier
reads the left neighbor set by the previous quantifer (e.g., L1 and
L2).
BOX: Of what use is the WANT quantifier?
BOX:
BOX: How do you specify a WANT quantifier that matches
BOX: phrases of lengths greater than one?
BOX:
BOX: How do you get WANT to match non-full-spanning phrases?
Figure 25.9(a) shows the ambiguous phrase if A, B, and C are all of
type REAL. Part (b) shows what is generated as a by-product of the
grammar.
The datatype rules relevant to this example are:
1) ~REAL ~REAL + -> ~REAL
2) ~POINT ~POINT + -> ~POINT
3) ~REAL ~REAL # -> ~POINT
("+" works on POINTs as well as REALs, and "#" combines two REALs to
form a POINT).
The two phrases making up the ambiguous phrase may or may not
individually parse successfully. For example, suppose the types of A,
B, and C are all REALs. The two phrases appear as:
~REAL ~REAL + ~REAL #
and
~REAL ~REAL ~REAL # +
The first phrase reduces to the following, by rule #1:
~REAL ~REAL #
Rule #3 reduces this successfully to a full-spanning:
~POINT
In contrast, our second phrase can be partially parsed, via rule #3,
to:
~REAL ~POINT +
This final form can be reduced no further. No full-spanning type can
be acquired from this phrase with our rules (barring other coercions).
We've just seen how a syntax ambiguity generates multiple datatype
phrases, some of which might die, being unable to be rendered as a
full-spanning type. Neither, either, or both phrases may succeed.
We've seen one phrase succeed and the other fail.
BOX: If A were of type POINT, what phrase(s) would
BOX: survive?
If the types of A, B, and C were as follows:
A is POINT
B and C are REALs
then the ambiguous phrase would be:
~POINT ~REAL + ~REAL #
~or
~POINT ~REAL ~REAL # +
The latter phrase would be the only survivor (as the "REAL REAL #" goes
to POINT).
If A, B, and C were all POINTs, neither phrase would
survive. If A were itself ambiguous, either a REAL or a POINT, while
B and C were still REALs, ~both phrases would survive.
25.5.4
Under Syntax, What Does The Semantic ~OR Block Do?
In Section 15.2 we characterized the action performed by the ~OR block
as being simply unspecified, a function by the name of F. We are now
in a position to choose a definition for F.
We want the ~OR block to generate an ambiguous phrase, the ambiguous
combination of the phrases generated by each of OR's two components.
We've seen already how to generate ambiguous phrases: Just generate
one phrase and then generate the other phrase. This is two
STATEMENTs executed sequentially, with no dash connecting them. Thus,
we define F via:
DEFINE F( A,B: BASIC_PROCESS ):
<*A*>;
<*B*>;
ENDDEFN
F invokes each of its given components, A, and B, so that each
contributes a phrase, where both phrases share the same span (LEFT and
C).
In figure 25.8(b), the OR-block invokes each of its constituents, and
thus generates the ambiguous phrase:
A B + C # ~or A B C # +
Figure 25.9 shows the generated phrase, if A, B, and C are REALs.
Thus, both syntactic and datatype ambiguities come together in one
formalism. Syntactic ambiguities generate ambiguous datatype phrases,
as also does the datatype grammar on its own. All ambiguities
ultimately reside in the datatype grammar.
BOX: How can ambiguities occur by the datatype grammar
BOX: alone?
BOX:
BOX: How does a syntactic ambiguity manifest itself in the
BOX: datatype language?
BOX:
BOX: What does the OR-block do during the execution of
BOX: syntax's semantics?
25.6
Picking Up The Generated Phrases As A CHOICE_OF_PHRASES
We generate phrases via STATEMENTs, as just shown. Once phrases are
generated, C holds all the phrases as a single CHOICE_OF_PHRASES.
We introduce two notations that turn ~any STATEMENT into a
CHOICE_OF_PHRASES. One of them is:
[-> STATEMENT <-] -> EXPR
(a CHOICE_OF_PHRASES)
This basically executes the STATEMENT and then yields the value
(the generated phrases in C).
This notation translates simply to:
HOLDING C:= NIL;
GIVE
DO ~the_STATEMENT
GIVE C
ENDHOLD
The STATEMENT is executed in a context where C is set to NIL initially.
All phrases generated, which wind up on C, is the value delivered by
this EXPR. (If the STATEMENT performs no phrase generation, then this
EXPR yields NIL).
This new EXPR depends on the variable LEFT. Whatever happens to be
in LEFT upon commencement of this EXPR's execution, will be the left
endpoint for all full-spanning phrases.
Our second notation will be the one we use here almost exclusively:
[> STATEMENT <] -> EXPR
This executes the STATEMENT, and yields ~almost all of
C as its result. It yields only the ~full-spanning phrases in C that
are of ~length ~one. Its translation follows:
HOLDING C:= NIL;
LEFT:= NIL;
GIVE
DO ~the_STATEMENT
GIVE C pruned so as to hold full-spanning unit-
length phrases only
ENDHOLD
Example:
The STATEMENT:
<INT>
generates a CHOICE_OF_PHRASES (on C) that includes at least an
<INT>. If the coercion from INT to REAL is a rule in our
datatype grammar, then C will also contain a <REAL>, sharing
the same span as the <INT>.
Let's enclose this STATEMENT within the "[>...<]":
[> <INT> <]
This EXPR is of type CHOICE_OF_PHRASES, and the value of this
EXPR is the CHOICE_OF_PHRASES that arises on C upon generating
the phrase <INT>. That is, this EXPR is a CHOICE_OF_PHRASES
containing both <INT> and <REAL>.
Example:
While the STATEMENT:
<A>
<B>
<C> - <D>
<E>
~generates the ambiguous phrase in figure 25.3, the EXPR:
[-> <A>
<B>
<C> - <D>
<E> <-]
delivers that generated phrase as a CHOICE_OF_PHRASES, with no
mention made of our variable C.
Our more popular operation with "[>" instead of "[->":
[> <A>
<B>
<C> - <D>
<E> <]
delivers only the full-spanning phrases A, B, and E.
(Conceivably, the "<C>-<D>" phrase, with a grammar active,
could produce other full-spanning phrases, which would then
be included).
Example:
Given the rules:
~INT ~INT plus -> ~INT
~REAL ~REAL plus -> ~REAL
~INT -> ~REAL
the CHOICE_OF_PHRASES delivered by:
[-> <INT> - <INT> - <plus> <-]
is shown in figure 25.7. The one delivered by:
[> <INT> - <INT> - <plus> <]
consists of only two phrases, the full-spanning INT and REAL.
BOX: BOX: What notations do we have that collect up the phrases
BOX: generated by the execution of a STATEMENT?
BOX:
BOX: The expression:
BOX:
BOX: [> <INT> <]
BOX:
BOX: represents what CHOICE_OF_PHRASES, assuming we have
BOX: the INT-to-REAL coercion?
BOX:
BOX: Because:
BOX:
BOX: <INT>
BOX:
BOX: is a STATEMENT, what effect does it have?
25.7
The WANT Quantifier
We now address the last notation required in order to present
a language involving two domains, in our case, syntax and
datatypes.
Suppose we have a CHOICE_OF_PHRASES and we want to find, say, a full-
spanning BOOLean. This need may arise in the implementation of the
syntax rule:
while EXPR ; -> QUANTIFIER
For this quantifier to be meaningful, the EXPR must be of type BOOL.
We can invoke that EXPR's semantics so as to generate all possible
types (phrases) that the EXPR could be interpreted as. Then, using
the notation "[>...<]", we obtain a CHOICE_OF_PHRASES that has all the
full-spanning types of that EXPR. We now are interested in that
full-spanning BOOL within the CHOICE_OF_PHRASES.
Suppose X is the CHOICE_OF_PHRASES. The ~new quantifier:
WANT <BOOL:B> FROM X ;
causes an iteration for each full-spanning BOOL in X. On each of
those iterations, it sets B to the semantics of the matched BOOL.
(According to Section 14.3, there can be at most one full-
spanning BOOL, as duplicate phrases are supressed. This
instance of the WANT quantifier thus causes always zero or one
iterations. It causes zero iterations if there is no full-
spanning BOOL, and one iteration otherwise).
This WANT quantifier translates into our more familiar FOR-quantifier:
FOR P $E X; WITH P.POS = BOOL &
-DEFINED( P.LEFT ) ;
EACH_DO b:= P.SEM ; ;
It looks at all phrase blocks (P) in the CHOICE_OF_PHRASES X, and
causes an iteration for each phrase block whose part-of-speech is BOOL,
and which is full-spanning (the "-defined(P.LEFT)"). It also sets the
matched phrase block's semantics into the variable B (the EACH_DO).
(The "P.SEM" here may be transformed to "<*P.SEM*>" if context
demands that).
The WANT quantifier is supported by the following syntax rule:
want TOKEN from EXPR ; -> QUANTIFER
The TOKEN is just like that admitted on the lefthand side of a rule.
The EXPR must be of type CHOICE_OF_PHRASES.
25.7.1
WANT Quantifier Can Involve Array Parts-Of-Speech
Recall that a TOKEN can be of the form:
< ID [ ID ] : ID >
as in:
<EXPR[I]:X> or <TYPES[T1]:X>
That is, for matching array parts-of-speech, the index variable (the ID
enclosed in "[...]") is also set upon each match.
For example, let's declare an array part-of-speech we will be using for
datatype processing:
POS TYPES[10000] : - ;
We will agree that any datatype is an instance of this TYPES array of
parts-of-speech. Therefore, the quantifier:
WANT <TYPES[T]:S> FROM X ;
may cause more than one iteration. Any part-of-speech that is a
member of the TYPES array of parts-of-speech will be matched, and T
will be set to its index, a different index for each match. We will
see examples of this use of the WANT quantifier in the next chapter.
25.7.2
WANT Can Match A Phrase
In general, the WANT quantifier can specify not only one TOKEN to
match, but a left-to-right sequence of TOKENs to be matched:
want TOKEN TOKEN ... TOKEN from EXPR ; -> QUANTIFIER
For example, consider:
WANT <REAL:a> <INT:b> <plus> FROM X ;
This will cause an iteration for each full-spanning occurence of the
phrase:
<REAL> <INT> <plus>
There will be one match if X is figure 25.7.
25.7.3
WANT Can Recognize Non-Full-Spanning Phrases
Finally, the WANT quantifier can be used even to find non-full-spanning
phrases. The left side of the phrase to match may be augmented via
the syntax:
ID --
as in:
WANT L-- <REAL:a> <INT:b> <plus> FROM X ;
Now all occurences of the phrase:
<REAL> <INT> <plus>
emenating from X will be matched. Upon each match, the new variable L
is set to the left neightbor of the matched phrase.
Now that we can capture the left neighbor of a matched phrase, we can
note an equivalence. For example, the quantifier:
WANT <REAL:a> <INT:b> <plus> FROM X ;
can be written equivalently as:
WANT L1-- <plus> FROM X ;
!!
WANT L2-- <INT:b> FROM L1 ;
!!
WANT <plus> FROM L2 ;
Each of these three quantifiers matches one token of the original
match phrase. Each token is not required to be full-spanning, as the
notation:
ID --
occurs in the first two quantifiers. Notice how the next quantifier
reads the left neighbor set by the previous quantifer (e.g., L1 and
L2).
BOX: Of what use is the WANT quantifier?
BOX:
BOX: How do you specify a WANT quantifier that matches
BOX: phrases of lengths greater than one?
BOX:
BOX: How do you get WANT to match non-full-spanning phrases?