CHAPTER 2
ACTION OR DELAYED SEMANTICS
Sometimes we prefer to specify semantics in terms of actions, not
values. For example, we might prefer that the semantics of FORM
perform the action of "writing itself out" to your terminal. That
is different from delivering an integer answer.
A compiler might wish to perform the action of "generate machine
language code", or "generate phrases in yet another language". That
is, instead of receiving some INTeger value from a <FORM>, we want some
specific action to occur.
2.1
BASIC_PROCESSes
We provide the type BASIC_PROCESS to represent actions. The type
BASIC_PROCESS, and process types in general are documented in more
detail in Section 21.4.5.4 and 23.6.
You use or ~invoke a BASIC_PROCESS by writing:
<* the_BASIC_PROCESS *> ;
This makes the action represented by the_BASIC_PROCESS happen.
You ~create a BASIC_PROCESS by enclosing some program text between
// and \\, as in:
//
WRITE('.');
\\
This BASIC_PROCESS's action is to write a period to your terminal.
Let us declare a variable of type BASIC_PROCESS:
VAR B = BASIC_PROCESS ;
Now we can write
B := // WRITE('.'); \\ ;
and
<* B *> ;
The former statement, the assignment into B, doesn't cause a period
to appear on your terminal. It merely puts into B the "seed", which
when invoked later, will cause a period to appear on the terminal.
The latest line invokes the BASIC_PROCESS in B, and hence writes a
period to the terminal.
Let's make each of FORM, TERM, and ATOM be a BASIC_PROCESS instead of
an INT. We erase the old declaration of FORM, TERM, and ATOM, and
write instead:
POS FORM, TERM, ATOM : BASIC_PROCESS ;
Now each of FORM, TERM, and ATOM has type BASIC_PROCESS, a type which
is different from the type INT still found in DIGIT and NUMBER.
Here is the formulas grammar again:
<ATOM: atomize(n) > ::= <NUMBER:n>
<ATOM: x > ::= ( <FORM:x> )
<TERM: x > ::= <ATOM:x>
<TERM: times(a,b) > ::= <TERM:a> * <ATOM:b>
<FORM: x > ::= <TERM:x>
<FORM: sum(a,b) > ::= <FORM:a> + <TERM:b>
We've introduced one difference: The first rule now calls a function,
ATOMIZE. This is necessary because the type of <NUMBER>, and hence
the type of the variable N, is INTeger. However ATOM demands a
BASIC_PROCESS instead. The appearence of N by itself would be
insufficient for the meaning of an <ATOM>. The function ATOMIZE is
there to turn an INT into a BASIC_PROCESS.
All we need to do now is to write the three functions:
ATOMIZE( INT ) -> BASIC_PROCESS
SUM( BASIC_PROCESS , BASIC_PROCESS ) -> BASIC_PROCESS
TIMES( BASIC_PROCESS , BASIC_PROCESS ) -> BASIC_PROCESS
ATOMIZE takes in an INT and yields a BASIC_PROCESS. Each of SUM and
TIMES maps a pair of BASIC_PROCESSs to a single BASIC_PROCESS. These
datatype constraints are dictated by the types we've declared with the
parts-of-speech FORM, TERM, ATOM, and NUMBER.
The definition for ATOMIZE is nearly:
DEFINE ATOMIZE( N:INT ) = BASIC_PROCESS:
//
WRITE(N);
\\
ENDDEFN
That is, ATOMIZE delivers a BASIC_PROCESS (//...\\) whose action is to
write out N.
We actually write
DEFINE ATOMIZE( N:INT ) = BASIC_PROCESS:
//[N;]
WRITE(N);
\\
ENDDEFN
We've inserted the text "[N;]" just after the //. This is necessary
so that the WRITE retains access to N. The //...\\ always denotes
a break in time. The future is inside the //...\\, and the present
is outside the //...\\. The "[N;]" transports N from the present into
the future. N exists in the present (while ATOMIZE is called), but
WRITE needs N in the future, when this resulting BASIC_PROCESS might
be invoked.
ATOMIZE(3) is thus a BASIC_PROCESS whose action is to write 3.
ATOMIZE(3) is the semantics of the <ATOM> interpretation for the
string:
3
Thus, the invocation of the <ATOM>'s semantics will cause a 3 to appear
on the terminal. Remember that a call to ATOMIZE merely delivers
the //...\\. The "..." in there is not executed when ATOMIZE is
called. ATOMIZE's result, the BASIC_PROCESS, can be invoked later.
Here is the definition for TIMES:
DEFINE TIMES( A,B:BASIC_PROCESS ) = BASIC_PROCESS:
//[A;B;]
WRITE('('); " write a '(' "
<*A*>; " make A write itself "
WRITE('*'); " the '*' "
<*B*>; " make B write itself "
WRITE(')'); " write the final ')' "
\\
ENDDEFN
The result of TIMES, the //...\\, retains access to A and B (the
"[A;B;]"), so that when it is invoked in the future, it can invoke
A and B so as to have them show themselves on the terminal.
TIME's resulting BASIC_PROCESS, when actually invoked, prints out
( ~what_A_is * ~what_B_is )
(Other formulas appear in the places of ~what_A_is and ~what_B_is).
Thus, the string 2*3 has semantics which when invoked, causes the
following to appear on the terminal:
(2*3)
(When TIMES was called, A had ATOMIZE(2) and B had ATOMIZE(3).
Hence the "<*A*>;" in TIMES causes the 2 to appear and "<*B*>;"
causes the 3 to appear. The parentheses and the "*" are printed
via the WRITE statements in the process delivered by TIMES).
SUM is the same, except that it writes a "+" instead of "*":
DEFINE SUM( A,B:BASIC_PROCESS ) = BASIC_PROCESS:
//[A;B;]
WRITE('(');
<*A*>;
WRITE('+');
<*B*>;
WRITE(')');
\\
ENDDEFN
The string 1+2*3 has semantics which when invoked, causes the
following to appear on the terminal:
(1+(2*3))
At the time SUM was called, A had the semantics of "1" and B had the
semantics of "2*3". The "<*B*>;" in SUM causes the "(2*3)" to be
printed.
We've written SUM and TIMES so as to always produce parentheses
around the "+" ("*") and its operands. The latest line exposes
explicitly that we group multiplications before additions.
2.2
Exercises
1) How will each of the following formulas appear on the terminal
when their semantics are invoked?
a) 5
b) ((5))
c) 2*(3+(4))
d) 2*3+4*5
e) 1+(2+(3+(4+5)))
2) Let's rewrite the definition of SUM as follows:
DEFINE SUM( A,B:BASIC_PROCESS ) = BASIC_PROCESS:
//[A;B;]
WRITE('(');
<*A*>;
WRITE('+');
<*A*>;
WRITE(')');
\\
ENDDEFN
What will appear on the terminal when we invoke the semantics
each of the following? It will be helpful to write down the
derivation for each:
a) 1+2
b) (1+2)+3
c) 1+2+3
d) 1+2*3+4
e) (1+2)*(3+4)
3) Rewrite ATOMIZE so that a space character appears before the
number.
4) Rewrite SUM and TIMES so as to produce prefix Polish notation,
where the operator (e.g., "+") appear not between its
operands, but before them. That is, we want:
1+2 to appear as + 1 2
2*3 to appear as * 2 3
1+2*3 to appear as + 1 * 2 3
2*3+4*5 to appear as + * 2 3 * 4 5
This polish notation needs no parentheses.
5) Why was it necessary to introduce the function ATOMIZE when
we chose BASIC_PROCESS as the type for FORM, TERM, and ATOM?
6) Consider the formulas grammar.
Why is it necessarily the case that the type of the result
of sum(x,y) is the same type as the data in x? Is this
true no matter what type we give for the semantics of FORM and
TERM? Is it conceivable that the type of y might be different
from the type of sum(x,y)?
7) Let's declare parts-of-speech as follows:
POS FORM, TERM, ATOM : REAL ;
We choose to leave INTegers behind and adopt REALs (floating
numbers, or numbers with fractions) so that we can introduce
the divide operator "/", as in the rule:
<TERM: a/b > ::= <TERM:a> / <ATOM:b>
We want the resulting a/b to be accurately represented. Assume
the following:
* Each of "+", "*", and "/" in our semantic language work
not only for INTegers, but also on REALs, as is the
case in many programming languages.
* There is the operator FLOAT which turns an INT into a
REAL, i.e.,
FLOAT( int ) -> real
a) Write the whole formulas grammar, with "/", so as to
be compatable with our new declarations for the parts-
of-speech FORM, TERM, and ATOM. (NUMBERs are still
INTegers).
b) Why have we introduced "/" by the rule
<TERM: a/b > ::= <TERM:a> / <ATOM:b>
instead of the rule
<FORM: a/b > ::= <FORM:a> / <TERM:b>
With the former rule, what is the value of 1+2/3?
With the latter rule, what is the value of 1+2/3?
8) Let's introduce a new part-of-speech:
POS FLOATING_NUMBER : REAL ;
We introduce the rule:
<FLOATING_NUMBER: ... > ::= <NUMBER:x> . <NUMBER:y>
The "..." is
DO continually divide y by 10, until it is less than
one.
GIVE x + y
As a <FLOATING_NUMBER>, what are the values of
a) 1.0
b) 1.7
c) 10.7
d) 1.07
Does this method work? If not, in what cases will it not
work?
�
2.3
More About Delayed Semantics
The type BASIC_PROCESS has two very useful properties:
1) It takes almost no time to create a BASIC_PROCESS.
(The //...\\ is very cheep to create, even when the
inside (...) is an expensive computation. That
expensive computation will happen later, upon
invocation, but not now, at the time of creation).
2) Even if the action represented by the BASIC_PROCESS has side-
effects, the action of creating of the BASIC_PROCESS has no
side-effects.
(The side-effects will occur later, when the
BASIC_PROCESS is invoked).
The generation of a BASIC_PROCESS is very fast and is free of side-
effects. This makes BASIC_PROCESS the ideal type for semantics, when
we consider that a parser may indeed try many false rewrites, rewrites
which won't be part of any overall meaning for the given string.
2.3.1
False Rewrites During Parsing
For example, a parser might at some time consider the following
rewrite sequence:
1 + 2 * 3
<DIGIT:1> <DIGIT:2> <DIGIT:3>
<NUMBER:1> <NUMBER:1> <NUMBER:1>
<ATOM: atomize(1)> <ATOM: atomize(2)> <ATOM: atomize(3)>
<TERM: atomize(1)> <TERM: atomize(2)> <TERM: atomize(3)>
<FORM: atomize(1)>
-- <FORM: sum(atomize(1),atomize(2))> --
This final <FORM> spanning the 1+2 cannot be used in any successful
derivation for 1+2*3. If sum were an expensive computation, the time
taken to compute sum(1,2) would be a major loss. In addition, if sum
involved side-effects, the side-effects would have to be undone at
some time.
We make sum both inexpensive and free of side-effects by
having sum return a BASIC_PROCESS, whose later execution will perform
the expensive computation and side-effects. In this
example, since sum(1,2) won't be part of any successful derivation
for 1+2*3, the program given by sum(1,2) will never be executed!
2.3.2
BASIC_PROCESS's Are Cheap
The BASIC_PROCESS is represented by the address of a program along
with its square-bracket context, the values held in the variables
appearing within the square-brackets. For example, the BASIC_PROCESS
//[A;B;]
WRITE('(');
<*A*>;
WRITE('+');
<*B*>;
WRITE(')'); \\
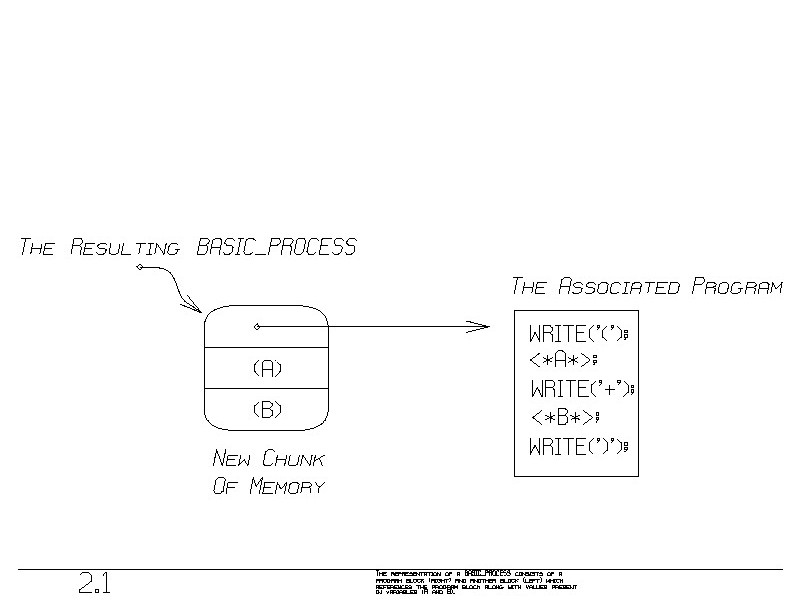 is represented as shown in figure 2.1.
Given the values presently in
the variables A and B, the creation of the BASIC_PROCESS is quick; it
merely allocates a chunk of memory and stuffs the values from A and B
into it. We also stuff in the address of the associated program.
(That address is represented in the figure by a pointer).
In these figures we use the notation
(A)
to mean a copy of what is in the variable A. In figure 2.1, we can see
that the present values of A and B are stuffed into the new chunk of
memory. Upon future invocations (<*...*>), those values will be put
back into A and B for the duration of the execution of the program
appearing on the right. (Between the time of creation and the time
of invocation, the variables A and B may lose their original values,
as A and B may be used for other purposes).
is represented as shown in figure 2.1.
Given the values presently in
the variables A and B, the creation of the BASIC_PROCESS is quick; it
merely allocates a chunk of memory and stuffs the values from A and B
into it. We also stuff in the address of the associated program.
(That address is represented in the figure by a pointer).
In these figures we use the notation
(A)
to mean a copy of what is in the variable A. In figure 2.1, we can see
that the present values of A and B are stuffed into the new chunk of
memory. Upon future invocations (<*...*>), those values will be put
back into A and B for the duration of the execution of the program
appearing on the right. (Between the time of creation and the time
of invocation, the variables A and B may lose their original values,
as A and B may be used for other purposes).
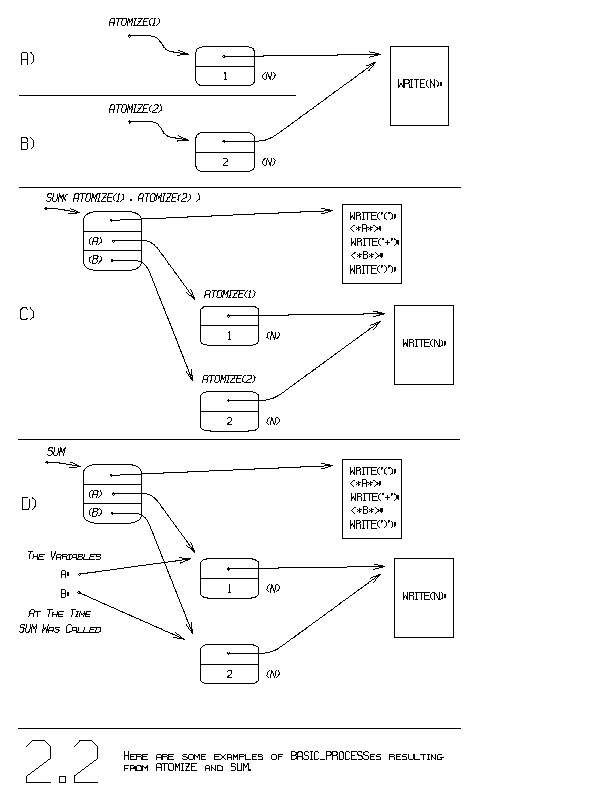 The results of ATOMIZE(1) and ATOMIZE(2) are shown in figure 2.2 parts
(a) and (b).
Each has its own new chunk of memory. Notice how each
holds a different value for N. Notice also that both results
reference the same occurence of the program, the "..." in //...\\,
the "WRITE(N);".
Figure 2.2(c) shows the result of
sum. That result references what the variables A and B reference, as
shown in figure 2.2(d). The call to SUM creates only one new memory
chunk, the one appearing in the upper left of figure 2.2(d). The last
two words in that memory chunk contain exactly what A and B contained
at the time SUM was called.
This simple operation of allocating a new memory chunk and putting
the values of A and B into it gives rise to complicated looking
diagrams. Because A and B each contains a pointer (the address of
another memory chunk), the newly allocated memory chunk winds up
holding those pointers. Thus, we wind up with memory chunks pointing
to other memory chunks, which themselves may point to others, etc.
Although these diagrams, intertwining data and programs, seem daunting,
the computer deals with them very easily and efficiently. Each block
is built easily. The composition of such blocks only ~looks
complicated. Fortunately, we don't have to think about that. These
figures are included so as to satisfy the reader who wants to
understand how these concepts are actually implemented in computer
memory. More about chunks of memory and pointers appears in Part 3.
Let's consider what happens upon the invocation of the result from
SUM (the upper left memory chunk in figure 2.2(d)). Simply by passing
the address of the SUM memory chunk into the invocation operator
(<*...*>), the invocation operator can do its thing. It calls
the associated program (whose address is in the first word), but first
puts back into A and B the contents of the memory chunk's second and
third bins.
That program execution will first write the "(", and
then invoke A. It is this second operation that has required the
preservation of A's original value. Once again, the "<*A*>;" merely
passes to the invocation operator the pointer residing in A. The
invocation operator does the same old thing: It restores the value 1
into the variable N, and executes the associated program, the
"WRITE(N);". Upon completion of "WRITE(N);", the "<*A*>;" in SUM
is complete. SUM's program then continues by writing the "+", and
then invoking B (the "<*B*>;"). The invocation operator, now given
the address in B, ultimately writes out the 2.
The results of ATOMIZE(1) and ATOMIZE(2) are shown in figure 2.2 parts
(a) and (b).
Each has its own new chunk of memory. Notice how each
holds a different value for N. Notice also that both results
reference the same occurence of the program, the "..." in //...\\,
the "WRITE(N);".
Figure 2.2(c) shows the result of
sum. That result references what the variables A and B reference, as
shown in figure 2.2(d). The call to SUM creates only one new memory
chunk, the one appearing in the upper left of figure 2.2(d). The last
two words in that memory chunk contain exactly what A and B contained
at the time SUM was called.
This simple operation of allocating a new memory chunk and putting
the values of A and B into it gives rise to complicated looking
diagrams. Because A and B each contains a pointer (the address of
another memory chunk), the newly allocated memory chunk winds up
holding those pointers. Thus, we wind up with memory chunks pointing
to other memory chunks, which themselves may point to others, etc.
Although these diagrams, intertwining data and programs, seem daunting,
the computer deals with them very easily and efficiently. Each block
is built easily. The composition of such blocks only ~looks
complicated. Fortunately, we don't have to think about that. These
figures are included so as to satisfy the reader who wants to
understand how these concepts are actually implemented in computer
memory. More about chunks of memory and pointers appears in Part 3.
Let's consider what happens upon the invocation of the result from
SUM (the upper left memory chunk in figure 2.2(d)). Simply by passing
the address of the SUM memory chunk into the invocation operator
(<*...*>), the invocation operator can do its thing. It calls
the associated program (whose address is in the first word), but first
puts back into A and B the contents of the memory chunk's second and
third bins.
That program execution will first write the "(", and
then invoke A. It is this second operation that has required the
preservation of A's original value. Once again, the "<*A*>;" merely
passes to the invocation operator the pointer residing in A. The
invocation operator does the same old thing: It restores the value 1
into the variable N, and executes the associated program, the
"WRITE(N);". Upon completion of "WRITE(N);", the "<*A*>;" in SUM
is complete. SUM's program then continues by writing the "+", and
then invoking B (the "<*B*>;"). The invocation operator, now given
the address in B, ultimately writes out the 2.
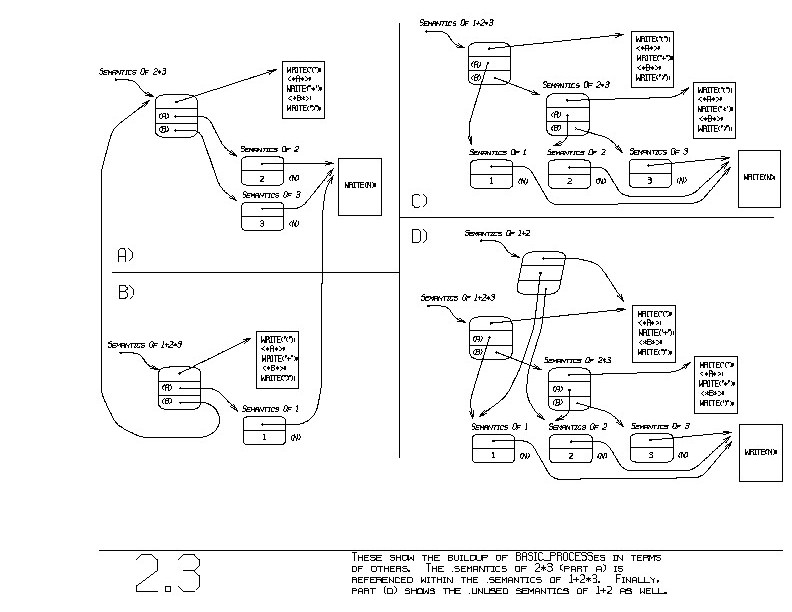 Figure 2.3(a) shows the semantics of 2*3.
Figure 2.3(b) shows the
semantics for 1+2*3. Notice how it references the semantics of 2*3
(the B parameter). The A parameter holds the semantics of "1".
Figure 2.3(c) shows an equivalent way of drawing the semantics of
1+2*3. Please study this carefully. Recall that when SUM was called,
A had the semantics of 1 and B had the semantics of 2*3.
We noted earlier that many false rewrites, rewrites that
lead nowhere, may be performed during parsing. Figure 2.3(d) shows the
semantics of 1+2*3 along with the semantics for the false rewrite of
1+2. Although we took the time to create the semantics of 1+2, it is
never referenced from within the semantics of the overall 1+2*3.
If you follow the arrows from 1+2*3, you will never arrive at the
semantics of 1+2. (You can reach each of 1 and 2, but not 1+2).
Not only will the semantics of 1+2
never be executed, the memory chunk used to represent it will soon
be reclaimed by a process called garbage collection (Part 8). Garbage
collection recycles memory chunks that are inaccessible. When we
ultimately hold on to only the semantics of 1+2*3, the 1+2 semantics
will be referenced by no one. It will be entirely safe to reuse those
memory chunks for other (future) uses. Thus, the semantics built up
for false rewrites will never be executed and will ultimately consume
no memory.
Thus, we keep false rewrites from being expensive by delaying the
bulk of execution of any semantics until the parsing is done. During
the parsing, only (cheap) BASIC_PROCESS's are created. Finally, when
the parsing is done, we execute only the semantics accessible from the
overall <FORM> spanning the input 1+2*3. The semantics of all false
rewrites simply do not exist within the overal <FORM>'s semantics.
2.3.3
The Transfer From Syntax To Action Semantics
So far, none of our rules in the formula grammar (with BASIC_PROCESS
semantics) invokes any BASIC_PROCESS immediately. All invocations
(<*...*>) appear inside of //...\\. That is, all invocations occur in
the future. There is no invocation outside any //...\\ to get things
started now in the present.
We now introduce a rule which will cause the semantics to be executed:
SHOW <FORM:f> . -> <*f*>;
The righthand side of the "->" is a program. That program is executed
as soon as the "SHOW <FORM> ." is seen. That immediate invocation of
f causes the <FORM> to show itself now on your terminal.
2.4
Top-Down Context
BASIC_PROCESSs allows us to control the executions of our constituents
(e.g., the ~a and ~b in SUM). We were able to write an open
parenthesis "(" prior to causing ~a to write itself.
We have the chance to "set things up" prior to any invocation. What
ever we set up prior to invocation is called ~top-down ~context for
that invocation. Top-down context is values put into certain variables
prior to an invocation. Those variables are then read during the
invocation.
For example, we could change part of the formula grammar so as to
print numbers in a base different from base ten. We declare a global
variable to hold the new context:
VAR WHICH_BASE = INT ; " (a variable of type INTeger)"
We will stick a value into WHICH_BASE prior to invoking any
BASIC_PROCESS.
First, let's make ATOMIZE respond to WHICH_BASE, with this
new definition for ATOMIZE:
DEFINE ATOMIZE( N:INT ) = BASIC_PROCESS:
//[N;]
WRITE_IN_BASE( N, WHICH_BASE ) ;
\\
ENDDEFN
This presumes there is a function that will write an INT in any
desired base, i.e.,
WRITE_IN_BASE( the_number , the_base )
The variable WHICH_BASE is a global variable, and hence doesn't need
to appear in the square-brackets ("[]") like the variable N (see
Section 21.4.5.4 or 23.6). That is, during the call to ATOMIZE, we
don't care at all about WHICH_BASE's present value. We use WHICH_BASE
only as a variable in the ~future, ~during ~invocations.
So far, we haven't put a value into WHICH_BASE. Let's set it now, to
the default base ten:
WHICH_BASE := 10 ;
Now, SHOW <FORM> will continue to work as before.
Let's add the rule:
SHOW <FORM:f> IN BASE <NUMBER:n> . -> ...
which does contain specification for a base. The righthand ... is
a program:
~HOLDING WHICH_BASE := N ;
~DO <*F*>;
~ENDHOLD
This rule invokes F after putting the correct base into WHICH_BASE.
We use the ~HOLDING construct because we don't want to have a permanent
effect on the global variable WHICH_BASE. We want merely a temporary
effect, long enough to cover the invocation of F. After the ENDHOLD,
WHICH_BASE goes back to its original value, e.g., ten. (Sections
21.4.2.2 or 22.1.10 or 22.2.2 tell more).
(This use of HOLDING is equivalent to:
OLD := WHICH_BASE; "Save the original value"
WHICH_BASE:= N;
<*F*>;
WHICH_BASE:= OLD; "Restore original value" )
2.4.1
Another Example Of Top-Down Context
The following example probably has no application, but it will further
illustrate top-down context. More realistic examples will follow in
Section 3.3.
For now, let's introduce a new, odd meaning for parentheses. Let's
suppose that parentheses not only imply a grouping, but that they also
change all numbers appearing between the parentheses. We would like
each pair of enclosing parentheses to cause all numbers within them
to be multiplied by a factor of ten. That is, we would like the
following printouts upon invoking semantics:
5 appears as 5
(5) appears as 50
((5)) appears as 500
1+(2*(3)) appears as (1+(20*300))
We change two rules:
<NUMBER:n> -> <ATOM: atomize(n) >
( <FORM:f> ) -> <ATOM: f >
We change the first rule so as to write numbers multiplied by some
power of 10, a value that we ~presume is in the new variable
THE_FACTOR:
<NUMBER:n> -> <ATOM: //[n;]
WRITE( n * THE_FACTOR );
\\ >
(We've abandoned the ATOMIZE function, but we've replaced the call
to ATOMIZE directly by what we'd otherwise put into a modified
rendition of ATOMIZE). The semantics of the <ATOM> is a BASIC_PROCESS
whose action is to write out N times THE_FACTOR.
We must declare the top-down context variable THE_FACTOR. We declare
it now:
VAR THE_FACTOR = INT ;
Prior to invoking any <ATOM>, we must set THE_FACTOR.
The updated parentheses rule sets THE_FACTOR:
( <FORM:f> ) ->
<ATOM: //[f;]
HOLDING THE_FACTOR:= THE_FACTOR*10;
DO <*f*>;
ENDHOLD
\\ >
This //...\\ in the <ATOM> is a BASIC_PROCESS (as is demanded by the
part-of-speech ATOM). Its action is to invoke F (the <FORM> between
the parentheses) under the illusion that THE_FACTOR is ten times
greater.
Once again, we use the HOLDING construct to
assign the new value into THE_FACTOR: We want this effect to exist
only during the invocation <*F*>. THE_FACTOR provides the
communication from this parentheses rule down to the semantics of
the <ATOM>, which prints numbers.
With this rule, we haven't taken the time to make up a new function,
say
DEFINE PAREN( F:BASIC_PROCESS ) = BASIC_PROCESS: ... ENDDEFN
We've written the body of the function instead of a call to the
function.
Before we start any of this, let's set THE_FACTOR's default value,
(the value that will reign outside any parentheses):
THE_FACTOR:= 1 ;
2.4.2
Exercises
1) What value will THE_FACTOR contain when we actually print out
the 5 in
(2+5)*3 ?
What about in
1+2*(3+(4)+5)
or
1+2*(3+(4+5)) ?
2) How will 1+2*(3+(4+5)) appear upon invocation of semantics?
3) Suppose we didn't use the HOLDING construct in the parentheses
rule. Suppose we wrote instead:
( <FORM:f> ) ->
<ATOM: //[f;]
THE_FACTOR:= THE_FACTOR*10;
<*f*>;
\\ >
How will (1)+(2) appear? How about 1+(2)+3?
What if we invoke the semantics of 1+(2+3) and then invoke
the semantics of 1? What will the lone 1 appear as? What if
we then invoke the semantics of 2+(3)? What will we see?
4) Modify the semantics of the <ATOM> in the previous excercise
so that without the HOLDING construct, THE_FACTOR will appear
on exit to contain the same value as it had upon entrance.
5) Rewrite the parentheses rule and the "+" rule (SUM) so that
within parentheses, "+" prints out its operands swapped, i.e.,
1+2 appears as (1+2)
1+(2+3) appears as (1+(3+2))
1+((2+3)) appears as (1+(3+2))
1+(2+(3+4)) appears as (1+((4+3)+2))
That is, the operand order is reversed for any expression
enclosed in one or more parentheses pairs. You will need to
declare a new global as follows:
VAR INSIDE_PARENS = BOOL ;
This is a Boolean variable. It can be assigned the values
TRUE and FALSE, and it can be used in the IF-THEN-ELSE
construct, e.g.,
IF INSIDE_PARENS THEN ...
ELSE ... FI
(The FI is part of the IF-THEN-ELSE notation, as shown in
Section 21.4.2.3 or 22.2.3).
First ask yourself which two rules need to be modified.
6) Instead of having parentheses multiply by ten everything
inside them, have them instead subtract one. We want
1+(3+4) to appear as (1+(2+3))
1+(3+(4)) to appear as (1+(2+2))
Modify two rules to make this so. You
can use the variable THE_FACTOR, although a better variable
name would be THE_DEBIT.
7) Consider now only the WHICH_BASE top-down context variable.
Consider the new rule:
<ATOM:a> IN BASE <NUMBER:n> ->
<ATOM: //[a;n;]
HOLDING WHICH_BASE:= n;
DO <*a*>;
ENDHOLD
\\ >
This rule allows an <ATOM> to be augmented with a new base
specification for print out. What will the following appear
as:
a) 5 IN BASE 2
b) 5+6 IN BASE 2
c) (5+6) IN BASE 2
d) 5+(6 IN BASE 2)
e) 5+6 IN BASE 2 * 3 IN BASE 3
f) 5 IN BASE 2 IN BASE 3
g) 5+6 IN BASE 2 IN BASE 3
It will be helpful to write down the derivation for each of
these expressions.
Suppose we change the new rule so that <FORM> appears instead
of <ATOM>:
<FORM:a> IN BASE <NUMBER:n> -> <FORM: ... >
(The "..." is unchanged). Which of the above formulas can
still be viewed as a <FORM>? How do those legal <FORM>s
appear when their semantics are invoked?
More practical examples of top-down context will appear in the next
chapter.
Figure 2.3(a) shows the semantics of 2*3.
Figure 2.3(b) shows the
semantics for 1+2*3. Notice how it references the semantics of 2*3
(the B parameter). The A parameter holds the semantics of "1".
Figure 2.3(c) shows an equivalent way of drawing the semantics of
1+2*3. Please study this carefully. Recall that when SUM was called,
A had the semantics of 1 and B had the semantics of 2*3.
We noted earlier that many false rewrites, rewrites that
lead nowhere, may be performed during parsing. Figure 2.3(d) shows the
semantics of 1+2*3 along with the semantics for the false rewrite of
1+2. Although we took the time to create the semantics of 1+2, it is
never referenced from within the semantics of the overall 1+2*3.
If you follow the arrows from 1+2*3, you will never arrive at the
semantics of 1+2. (You can reach each of 1 and 2, but not 1+2).
Not only will the semantics of 1+2
never be executed, the memory chunk used to represent it will soon
be reclaimed by a process called garbage collection (Part 8). Garbage
collection recycles memory chunks that are inaccessible. When we
ultimately hold on to only the semantics of 1+2*3, the 1+2 semantics
will be referenced by no one. It will be entirely safe to reuse those
memory chunks for other (future) uses. Thus, the semantics built up
for false rewrites will never be executed and will ultimately consume
no memory.
Thus, we keep false rewrites from being expensive by delaying the
bulk of execution of any semantics until the parsing is done. During
the parsing, only (cheap) BASIC_PROCESS's are created. Finally, when
the parsing is done, we execute only the semantics accessible from the
overall <FORM> spanning the input 1+2*3. The semantics of all false
rewrites simply do not exist within the overal <FORM>'s semantics.
2.3.3
The Transfer From Syntax To Action Semantics
So far, none of our rules in the formula grammar (with BASIC_PROCESS
semantics) invokes any BASIC_PROCESS immediately. All invocations
(<*...*>) appear inside of //...\\. That is, all invocations occur in
the future. There is no invocation outside any //...\\ to get things
started now in the present.
We now introduce a rule which will cause the semantics to be executed:
SHOW <FORM:f> . -> <*f*>;
The righthand side of the "->" is a program. That program is executed
as soon as the "SHOW <FORM> ." is seen. That immediate invocation of
f causes the <FORM> to show itself now on your terminal.
2.4
Top-Down Context
BASIC_PROCESSs allows us to control the executions of our constituents
(e.g., the ~a and ~b in SUM). We were able to write an open
parenthesis "(" prior to causing ~a to write itself.
We have the chance to "set things up" prior to any invocation. What
ever we set up prior to invocation is called ~top-down ~context for
that invocation. Top-down context is values put into certain variables
prior to an invocation. Those variables are then read during the
invocation.
For example, we could change part of the formula grammar so as to
print numbers in a base different from base ten. We declare a global
variable to hold the new context:
VAR WHICH_BASE = INT ; " (a variable of type INTeger)"
We will stick a value into WHICH_BASE prior to invoking any
BASIC_PROCESS.
First, let's make ATOMIZE respond to WHICH_BASE, with this
new definition for ATOMIZE:
DEFINE ATOMIZE( N:INT ) = BASIC_PROCESS:
//[N;]
WRITE_IN_BASE( N, WHICH_BASE ) ;
\\
ENDDEFN
This presumes there is a function that will write an INT in any
desired base, i.e.,
WRITE_IN_BASE( the_number , the_base )
The variable WHICH_BASE is a global variable, and hence doesn't need
to appear in the square-brackets ("[]") like the variable N (see
Section 21.4.5.4 or 23.6). That is, during the call to ATOMIZE, we
don't care at all about WHICH_BASE's present value. We use WHICH_BASE
only as a variable in the ~future, ~during ~invocations.
So far, we haven't put a value into WHICH_BASE. Let's set it now, to
the default base ten:
WHICH_BASE := 10 ;
Now, SHOW <FORM> will continue to work as before.
Let's add the rule:
SHOW <FORM:f> IN BASE <NUMBER:n> . -> ...
which does contain specification for a base. The righthand ... is
a program:
~HOLDING WHICH_BASE := N ;
~DO <*F*>;
~ENDHOLD
This rule invokes F after putting the correct base into WHICH_BASE.
We use the ~HOLDING construct because we don't want to have a permanent
effect on the global variable WHICH_BASE. We want merely a temporary
effect, long enough to cover the invocation of F. After the ENDHOLD,
WHICH_BASE goes back to its original value, e.g., ten. (Sections
21.4.2.2 or 22.1.10 or 22.2.2 tell more).
(This use of HOLDING is equivalent to:
OLD := WHICH_BASE; "Save the original value"
WHICH_BASE:= N;
<*F*>;
WHICH_BASE:= OLD; "Restore original value" )
2.4.1
Another Example Of Top-Down Context
The following example probably has no application, but it will further
illustrate top-down context. More realistic examples will follow in
Section 3.3.
For now, let's introduce a new, odd meaning for parentheses. Let's
suppose that parentheses not only imply a grouping, but that they also
change all numbers appearing between the parentheses. We would like
each pair of enclosing parentheses to cause all numbers within them
to be multiplied by a factor of ten. That is, we would like the
following printouts upon invoking semantics:
5 appears as 5
(5) appears as 50
((5)) appears as 500
1+(2*(3)) appears as (1+(20*300))
We change two rules:
<NUMBER:n> -> <ATOM: atomize(n) >
( <FORM:f> ) -> <ATOM: f >
We change the first rule so as to write numbers multiplied by some
power of 10, a value that we ~presume is in the new variable
THE_FACTOR:
<NUMBER:n> -> <ATOM: //[n;]
WRITE( n * THE_FACTOR );
\\ >
(We've abandoned the ATOMIZE function, but we've replaced the call
to ATOMIZE directly by what we'd otherwise put into a modified
rendition of ATOMIZE). The semantics of the <ATOM> is a BASIC_PROCESS
whose action is to write out N times THE_FACTOR.
We must declare the top-down context variable THE_FACTOR. We declare
it now:
VAR THE_FACTOR = INT ;
Prior to invoking any <ATOM>, we must set THE_FACTOR.
The updated parentheses rule sets THE_FACTOR:
( <FORM:f> ) ->
<ATOM: //[f;]
HOLDING THE_FACTOR:= THE_FACTOR*10;
DO <*f*>;
ENDHOLD
\\ >
This //...\\ in the <ATOM> is a BASIC_PROCESS (as is demanded by the
part-of-speech ATOM). Its action is to invoke F (the <FORM> between
the parentheses) under the illusion that THE_FACTOR is ten times
greater.
Once again, we use the HOLDING construct to
assign the new value into THE_FACTOR: We want this effect to exist
only during the invocation <*F*>. THE_FACTOR provides the
communication from this parentheses rule down to the semantics of
the <ATOM>, which prints numbers.
With this rule, we haven't taken the time to make up a new function,
say
DEFINE PAREN( F:BASIC_PROCESS ) = BASIC_PROCESS: ... ENDDEFN
We've written the body of the function instead of a call to the
function.
Before we start any of this, let's set THE_FACTOR's default value,
(the value that will reign outside any parentheses):
THE_FACTOR:= 1 ;
2.4.2
Exercises
1) What value will THE_FACTOR contain when we actually print out
the 5 in
(2+5)*3 ?
What about in
1+2*(3+(4)+5)
or
1+2*(3+(4+5)) ?
2) How will 1+2*(3+(4+5)) appear upon invocation of semantics?
3) Suppose we didn't use the HOLDING construct in the parentheses
rule. Suppose we wrote instead:
( <FORM:f> ) ->
<ATOM: //[f;]
THE_FACTOR:= THE_FACTOR*10;
<*f*>;
\\ >
How will (1)+(2) appear? How about 1+(2)+3?
What if we invoke the semantics of 1+(2+3) and then invoke
the semantics of 1? What will the lone 1 appear as? What if
we then invoke the semantics of 2+(3)? What will we see?
4) Modify the semantics of the <ATOM> in the previous excercise
so that without the HOLDING construct, THE_FACTOR will appear
on exit to contain the same value as it had upon entrance.
5) Rewrite the parentheses rule and the "+" rule (SUM) so that
within parentheses, "+" prints out its operands swapped, i.e.,
1+2 appears as (1+2)
1+(2+3) appears as (1+(3+2))
1+((2+3)) appears as (1+(3+2))
1+(2+(3+4)) appears as (1+((4+3)+2))
That is, the operand order is reversed for any expression
enclosed in one or more parentheses pairs. You will need to
declare a new global as follows:
VAR INSIDE_PARENS = BOOL ;
This is a Boolean variable. It can be assigned the values
TRUE and FALSE, and it can be used in the IF-THEN-ELSE
construct, e.g.,
IF INSIDE_PARENS THEN ...
ELSE ... FI
(The FI is part of the IF-THEN-ELSE notation, as shown in
Section 21.4.2.3 or 22.2.3).
First ask yourself which two rules need to be modified.
6) Instead of having parentheses multiply by ten everything
inside them, have them instead subtract one. We want
1+(3+4) to appear as (1+(2+3))
1+(3+(4)) to appear as (1+(2+2))
Modify two rules to make this so. You
can use the variable THE_FACTOR, although a better variable
name would be THE_DEBIT.
7) Consider now only the WHICH_BASE top-down context variable.
Consider the new rule:
<ATOM:a> IN BASE <NUMBER:n> ->
<ATOM: //[a;n;]
HOLDING WHICH_BASE:= n;
DO <*a*>;
ENDHOLD
\\ >
This rule allows an <ATOM> to be augmented with a new base
specification for print out. What will the following appear
as:
a) 5 IN BASE 2
b) 5+6 IN BASE 2
c) (5+6) IN BASE 2
d) 5+(6 IN BASE 2)
e) 5+6 IN BASE 2 * 3 IN BASE 3
f) 5 IN BASE 2 IN BASE 3
g) 5+6 IN BASE 2 IN BASE 3
It will be helpful to write down the derivation for each of
these expressions.
Suppose we change the new rule so that <FORM> appears instead
of <ATOM>:
<FORM:a> IN BASE <NUMBER:n> -> <FORM: ... >
(The "..." is unchanged). Which of the above formulas can
still be viewed as a <FORM>? How do those legal <FORM>s
appear when their semantics are invoked?
More practical examples of top-down context will appear in the next
chapter.
 is represented as shown in figure 2.1.
Given the values presently in
the variables A and B, the creation of the BASIC_PROCESS is quick; it
merely allocates a chunk of memory and stuffs the values from A and B
into it. We also stuff in the address of the associated program.
(That address is represented in the figure by a pointer).
In these figures we use the notation
(A)
to mean a copy of what is in the variable A. In figure 2.1, we can see
that the present values of A and B are stuffed into the new chunk of
memory. Upon future invocations (<*...*>), those values will be put
back into A and B for the duration of the execution of the program
appearing on the right. (Between the time of creation and the time
of invocation, the variables A and B may lose their original values,
as A and B may be used for other purposes).
is represented as shown in figure 2.1.
Given the values presently in
the variables A and B, the creation of the BASIC_PROCESS is quick; it
merely allocates a chunk of memory and stuffs the values from A and B
into it. We also stuff in the address of the associated program.
(That address is represented in the figure by a pointer).
In these figures we use the notation
(A)
to mean a copy of what is in the variable A. In figure 2.1, we can see
that the present values of A and B are stuffed into the new chunk of
memory. Upon future invocations (<*...*>), those values will be put
back into A and B for the duration of the execution of the program
appearing on the right. (Between the time of creation and the time
of invocation, the variables A and B may lose their original values,
as A and B may be used for other purposes).
 The results of ATOMIZE(1) and ATOMIZE(2) are shown in figure 2.2 parts
(a) and (b).
Each has its own new chunk of memory. Notice how each
holds a different value for N. Notice also that both results
reference the same occurence of the program, the "..." in //...\\,
the "WRITE(N);".
Figure 2.2(c) shows the result of
sum. That result references what the variables A and B reference, as
shown in figure 2.2(d). The call to SUM creates only one new memory
chunk, the one appearing in the upper left of figure 2.2(d). The last
two words in that memory chunk contain exactly what A and B contained
at the time SUM was called.
This simple operation of allocating a new memory chunk and putting
the values of A and B into it gives rise to complicated looking
diagrams. Because A and B each contains a pointer (the address of
another memory chunk), the newly allocated memory chunk winds up
holding those pointers. Thus, we wind up with memory chunks pointing
to other memory chunks, which themselves may point to others, etc.
Although these diagrams, intertwining data and programs, seem daunting,
the computer deals with them very easily and efficiently. Each block
is built easily. The composition of such blocks only ~looks
complicated. Fortunately, we don't have to think about that. These
figures are included so as to satisfy the reader who wants to
understand how these concepts are actually implemented in computer
memory. More about chunks of memory and pointers appears in Part 3.
Let's consider what happens upon the invocation of the result from
SUM (the upper left memory chunk in figure 2.2(d)). Simply by passing
the address of the SUM memory chunk into the invocation operator
(<*...*>), the invocation operator can do its thing. It calls
the associated program (whose address is in the first word), but first
puts back into A and B the contents of the memory chunk's second and
third bins.
That program execution will first write the "(", and
then invoke A. It is this second operation that has required the
preservation of A's original value. Once again, the "<*A*>;" merely
passes to the invocation operator the pointer residing in A. The
invocation operator does the same old thing: It restores the value 1
into the variable N, and executes the associated program, the
"WRITE(N);". Upon completion of "WRITE(N);", the "<*A*>;" in SUM
is complete. SUM's program then continues by writing the "+", and
then invoking B (the "<*B*>;"). The invocation operator, now given
the address in B, ultimately writes out the 2.
The results of ATOMIZE(1) and ATOMIZE(2) are shown in figure 2.2 parts
(a) and (b).
Each has its own new chunk of memory. Notice how each
holds a different value for N. Notice also that both results
reference the same occurence of the program, the "..." in //...\\,
the "WRITE(N);".
Figure 2.2(c) shows the result of
sum. That result references what the variables A and B reference, as
shown in figure 2.2(d). The call to SUM creates only one new memory
chunk, the one appearing in the upper left of figure 2.2(d). The last
two words in that memory chunk contain exactly what A and B contained
at the time SUM was called.
This simple operation of allocating a new memory chunk and putting
the values of A and B into it gives rise to complicated looking
diagrams. Because A and B each contains a pointer (the address of
another memory chunk), the newly allocated memory chunk winds up
holding those pointers. Thus, we wind up with memory chunks pointing
to other memory chunks, which themselves may point to others, etc.
Although these diagrams, intertwining data and programs, seem daunting,
the computer deals with them very easily and efficiently. Each block
is built easily. The composition of such blocks only ~looks
complicated. Fortunately, we don't have to think about that. These
figures are included so as to satisfy the reader who wants to
understand how these concepts are actually implemented in computer
memory. More about chunks of memory and pointers appears in Part 3.
Let's consider what happens upon the invocation of the result from
SUM (the upper left memory chunk in figure 2.2(d)). Simply by passing
the address of the SUM memory chunk into the invocation operator
(<*...*>), the invocation operator can do its thing. It calls
the associated program (whose address is in the first word), but first
puts back into A and B the contents of the memory chunk's second and
third bins.
That program execution will first write the "(", and
then invoke A. It is this second operation that has required the
preservation of A's original value. Once again, the "<*A*>;" merely
passes to the invocation operator the pointer residing in A. The
invocation operator does the same old thing: It restores the value 1
into the variable N, and executes the associated program, the
"WRITE(N);". Upon completion of "WRITE(N);", the "<*A*>;" in SUM
is complete. SUM's program then continues by writing the "+", and
then invoking B (the "<*B*>;"). The invocation operator, now given
the address in B, ultimately writes out the 2.
 Figure 2.3(a) shows the semantics of 2*3.
Figure 2.3(b) shows the
semantics for 1+2*3. Notice how it references the semantics of 2*3
(the B parameter). The A parameter holds the semantics of "1".
Figure 2.3(c) shows an equivalent way of drawing the semantics of
1+2*3. Please study this carefully. Recall that when SUM was called,
A had the semantics of 1 and B had the semantics of 2*3.
We noted earlier that many false rewrites, rewrites that
lead nowhere, may be performed during parsing. Figure 2.3(d) shows the
semantics of 1+2*3 along with the semantics for the false rewrite of
1+2. Although we took the time to create the semantics of 1+2, it is
never referenced from within the semantics of the overall 1+2*3.
If you follow the arrows from 1+2*3, you will never arrive at the
semantics of 1+2. (You can reach each of 1 and 2, but not 1+2).
Not only will the semantics of 1+2
never be executed, the memory chunk used to represent it will soon
be reclaimed by a process called garbage collection (Part 8). Garbage
collection recycles memory chunks that are inaccessible. When we
ultimately hold on to only the semantics of 1+2*3, the 1+2 semantics
will be referenced by no one. It will be entirely safe to reuse those
memory chunks for other (future) uses. Thus, the semantics built up
for false rewrites will never be executed and will ultimately consume
no memory.
Thus, we keep false rewrites from being expensive by delaying the
bulk of execution of any semantics until the parsing is done. During
the parsing, only (cheap) BASIC_PROCESS's are created. Finally, when
the parsing is done, we execute only the semantics accessible from the
overall <FORM> spanning the input 1+2*3. The semantics of all false
rewrites simply do not exist within the overal <FORM>'s semantics.
2.3.3
The Transfer From Syntax To Action Semantics
So far, none of our rules in the formula grammar (with BASIC_PROCESS
semantics) invokes any BASIC_PROCESS immediately. All invocations
(<*...*>) appear inside of //...\\. That is, all invocations occur in
the future. There is no invocation outside any //...\\ to get things
started now in the present.
We now introduce a rule which will cause the semantics to be executed:
SHOW <FORM:f> . -> <*f*>;
The righthand side of the "->" is a program. That program is executed
as soon as the "SHOW <FORM> ." is seen. That immediate invocation of
f causes the <FORM> to show itself now on your terminal.
2.4
Top-Down Context
BASIC_PROCESSs allows us to control the executions of our constituents
(e.g., the ~a and ~b in SUM). We were able to write an open
parenthesis "(" prior to causing ~a to write itself.
We have the chance to "set things up" prior to any invocation. What
ever we set up prior to invocation is called ~top-down ~context for
that invocation. Top-down context is values put into certain variables
prior to an invocation. Those variables are then read during the
invocation.
For example, we could change part of the formula grammar so as to
print numbers in a base different from base ten. We declare a global
variable to hold the new context:
VAR WHICH_BASE = INT ; " (a variable of type INTeger)"
We will stick a value into WHICH_BASE prior to invoking any
BASIC_PROCESS.
First, let's make ATOMIZE respond to WHICH_BASE, with this
new definition for ATOMIZE:
DEFINE ATOMIZE( N:INT ) = BASIC_PROCESS:
//[N;]
WRITE_IN_BASE( N, WHICH_BASE ) ;
\\
ENDDEFN
This presumes there is a function that will write an INT in any
desired base, i.e.,
WRITE_IN_BASE( the_number , the_base )
The variable WHICH_BASE is a global variable, and hence doesn't need
to appear in the square-brackets ("[]") like the variable N (see
Section 21.4.5.4 or 23.6). That is, during the call to ATOMIZE, we
don't care at all about WHICH_BASE's present value. We use WHICH_BASE
only as a variable in the ~future, ~during ~invocations.
So far, we haven't put a value into WHICH_BASE. Let's set it now, to
the default base ten:
WHICH_BASE := 10 ;
Now, SHOW <FORM> will continue to work as before.
Let's add the rule:
SHOW <FORM:f> IN BASE <NUMBER:n> . -> ...
which does contain specification for a base. The righthand ... is
a program:
~HOLDING WHICH_BASE := N ;
~DO <*F*>;
~ENDHOLD
This rule invokes F after putting the correct base into WHICH_BASE.
We use the ~HOLDING construct because we don't want to have a permanent
effect on the global variable WHICH_BASE. We want merely a temporary
effect, long enough to cover the invocation of F. After the ENDHOLD,
WHICH_BASE goes back to its original value, e.g., ten. (Sections
21.4.2.2 or 22.1.10 or 22.2.2 tell more).
(This use of HOLDING is equivalent to:
OLD := WHICH_BASE; "Save the original value"
WHICH_BASE:= N;
<*F*>;
WHICH_BASE:= OLD; "Restore original value" )
2.4.1
Another Example Of Top-Down Context
The following example probably has no application, but it will further
illustrate top-down context. More realistic examples will follow in
Section 3.3.
For now, let's introduce a new, odd meaning for parentheses. Let's
suppose that parentheses not only imply a grouping, but that they also
change all numbers appearing between the parentheses. We would like
each pair of enclosing parentheses to cause all numbers within them
to be multiplied by a factor of ten. That is, we would like the
following printouts upon invoking semantics:
5 appears as 5
(5) appears as 50
((5)) appears as 500
1+(2*(3)) appears as (1+(20*300))
We change two rules:
<NUMBER:n> -> <ATOM: atomize(n) >
( <FORM:f> ) -> <ATOM: f >
We change the first rule so as to write numbers multiplied by some
power of 10, a value that we ~presume is in the new variable
THE_FACTOR:
<NUMBER:n> -> <ATOM: //[n;]
WRITE( n * THE_FACTOR );
\\ >
(We've abandoned the ATOMIZE function, but we've replaced the call
to ATOMIZE directly by what we'd otherwise put into a modified
rendition of ATOMIZE). The semantics of the <ATOM> is a BASIC_PROCESS
whose action is to write out N times THE_FACTOR.
We must declare the top-down context variable THE_FACTOR. We declare
it now:
VAR THE_FACTOR = INT ;
Prior to invoking any <ATOM>, we must set THE_FACTOR.
The updated parentheses rule sets THE_FACTOR:
( <FORM:f> ) ->
<ATOM: //[f;]
HOLDING THE_FACTOR:= THE_FACTOR*10;
DO <*f*>;
ENDHOLD
\\ >
This //...\\ in the <ATOM> is a BASIC_PROCESS (as is demanded by the
part-of-speech ATOM). Its action is to invoke F (the <FORM> between
the parentheses) under the illusion that THE_FACTOR is ten times
greater.
Once again, we use the HOLDING construct to
assign the new value into THE_FACTOR: We want this effect to exist
only during the invocation <*F*>. THE_FACTOR provides the
communication from this parentheses rule down to the semantics of
the <ATOM>, which prints numbers.
With this rule, we haven't taken the time to make up a new function,
say
DEFINE PAREN( F:BASIC_PROCESS ) = BASIC_PROCESS: ... ENDDEFN
We've written the body of the function instead of a call to the
function.
Before we start any of this, let's set THE_FACTOR's default value,
(the value that will reign outside any parentheses):
THE_FACTOR:= 1 ;
2.4.2
Exercises
1) What value will THE_FACTOR contain when we actually print out
the 5 in
(2+5)*3 ?
What about in
1+2*(3+(4)+5)
or
1+2*(3+(4+5)) ?
2) How will 1+2*(3+(4+5)) appear upon invocation of semantics?
3) Suppose we didn't use the HOLDING construct in the parentheses
rule. Suppose we wrote instead:
( <FORM:f> ) ->
<ATOM: //[f;]
THE_FACTOR:= THE_FACTOR*10;
<*f*>;
\\ >
How will (1)+(2) appear? How about 1+(2)+3?
What if we invoke the semantics of 1+(2+3) and then invoke
the semantics of 1? What will the lone 1 appear as? What if
we then invoke the semantics of 2+(3)? What will we see?
4) Modify the semantics of the <ATOM> in the previous excercise
so that without the HOLDING construct, THE_FACTOR will appear
on exit to contain the same value as it had upon entrance.
5) Rewrite the parentheses rule and the "+" rule (SUM) so that
within parentheses, "+" prints out its operands swapped, i.e.,
1+2 appears as (1+2)
1+(2+3) appears as (1+(3+2))
1+((2+3)) appears as (1+(3+2))
1+(2+(3+4)) appears as (1+((4+3)+2))
That is, the operand order is reversed for any expression
enclosed in one or more parentheses pairs. You will need to
declare a new global as follows:
VAR INSIDE_PARENS = BOOL ;
This is a Boolean variable. It can be assigned the values
TRUE and FALSE, and it can be used in the IF-THEN-ELSE
construct, e.g.,
IF INSIDE_PARENS THEN ...
ELSE ... FI
(The FI is part of the IF-THEN-ELSE notation, as shown in
Section 21.4.2.3 or 22.2.3).
First ask yourself which two rules need to be modified.
6) Instead of having parentheses multiply by ten everything
inside them, have them instead subtract one. We want
1+(3+4) to appear as (1+(2+3))
1+(3+(4)) to appear as (1+(2+2))
Modify two rules to make this so. You
can use the variable THE_FACTOR, although a better variable
name would be THE_DEBIT.
7) Consider now only the WHICH_BASE top-down context variable.
Consider the new rule:
<ATOM:a> IN BASE <NUMBER:n> ->
<ATOM: //[a;n;]
HOLDING WHICH_BASE:= n;
DO <*a*>;
ENDHOLD
\\ >
This rule allows an <ATOM> to be augmented with a new base
specification for print out. What will the following appear
as:
a) 5 IN BASE 2
b) 5+6 IN BASE 2
c) (5+6) IN BASE 2
d) 5+(6 IN BASE 2)
e) 5+6 IN BASE 2 * 3 IN BASE 3
f) 5 IN BASE 2 IN BASE 3
g) 5+6 IN BASE 2 IN BASE 3
It will be helpful to write down the derivation for each of
these expressions.
Suppose we change the new rule so that <FORM> appears instead
of <ATOM>:
<FORM:a> IN BASE <NUMBER:n> -> <FORM: ... >
(The "..." is unchanged). Which of the above formulas can
still be viewed as a <FORM>? How do those legal <FORM>s
appear when their semantics are invoked?
More practical examples of top-down context will appear in the next
chapter.
Figure 2.3(a) shows the semantics of 2*3.
Figure 2.3(b) shows the
semantics for 1+2*3. Notice how it references the semantics of 2*3
(the B parameter). The A parameter holds the semantics of "1".
Figure 2.3(c) shows an equivalent way of drawing the semantics of
1+2*3. Please study this carefully. Recall that when SUM was called,
A had the semantics of 1 and B had the semantics of 2*3.
We noted earlier that many false rewrites, rewrites that
lead nowhere, may be performed during parsing. Figure 2.3(d) shows the
semantics of 1+2*3 along with the semantics for the false rewrite of
1+2. Although we took the time to create the semantics of 1+2, it is
never referenced from within the semantics of the overall 1+2*3.
If you follow the arrows from 1+2*3, you will never arrive at the
semantics of 1+2. (You can reach each of 1 and 2, but not 1+2).
Not only will the semantics of 1+2
never be executed, the memory chunk used to represent it will soon
be reclaimed by a process called garbage collection (Part 8). Garbage
collection recycles memory chunks that are inaccessible. When we
ultimately hold on to only the semantics of 1+2*3, the 1+2 semantics
will be referenced by no one. It will be entirely safe to reuse those
memory chunks for other (future) uses. Thus, the semantics built up
for false rewrites will never be executed and will ultimately consume
no memory.
Thus, we keep false rewrites from being expensive by delaying the
bulk of execution of any semantics until the parsing is done. During
the parsing, only (cheap) BASIC_PROCESS's are created. Finally, when
the parsing is done, we execute only the semantics accessible from the
overall <FORM> spanning the input 1+2*3. The semantics of all false
rewrites simply do not exist within the overal <FORM>'s semantics.
2.3.3
The Transfer From Syntax To Action Semantics
So far, none of our rules in the formula grammar (with BASIC_PROCESS
semantics) invokes any BASIC_PROCESS immediately. All invocations
(<*...*>) appear inside of //...\\. That is, all invocations occur in
the future. There is no invocation outside any //...\\ to get things
started now in the present.
We now introduce a rule which will cause the semantics to be executed:
SHOW <FORM:f> . -> <*f*>;
The righthand side of the "->" is a program. That program is executed
as soon as the "SHOW <FORM> ." is seen. That immediate invocation of
f causes the <FORM> to show itself now on your terminal.
2.4
Top-Down Context
BASIC_PROCESSs allows us to control the executions of our constituents
(e.g., the ~a and ~b in SUM). We were able to write an open
parenthesis "(" prior to causing ~a to write itself.
We have the chance to "set things up" prior to any invocation. What
ever we set up prior to invocation is called ~top-down ~context for
that invocation. Top-down context is values put into certain variables
prior to an invocation. Those variables are then read during the
invocation.
For example, we could change part of the formula grammar so as to
print numbers in a base different from base ten. We declare a global
variable to hold the new context:
VAR WHICH_BASE = INT ; " (a variable of type INTeger)"
We will stick a value into WHICH_BASE prior to invoking any
BASIC_PROCESS.
First, let's make ATOMIZE respond to WHICH_BASE, with this
new definition for ATOMIZE:
DEFINE ATOMIZE( N:INT ) = BASIC_PROCESS:
//[N;]
WRITE_IN_BASE( N, WHICH_BASE ) ;
\\
ENDDEFN
This presumes there is a function that will write an INT in any
desired base, i.e.,
WRITE_IN_BASE( the_number , the_base )
The variable WHICH_BASE is a global variable, and hence doesn't need
to appear in the square-brackets ("[]") like the variable N (see
Section 21.4.5.4 or 23.6). That is, during the call to ATOMIZE, we
don't care at all about WHICH_BASE's present value. We use WHICH_BASE
only as a variable in the ~future, ~during ~invocations.
So far, we haven't put a value into WHICH_BASE. Let's set it now, to
the default base ten:
WHICH_BASE := 10 ;
Now, SHOW <FORM> will continue to work as before.
Let's add the rule:
SHOW <FORM:f> IN BASE <NUMBER:n> . -> ...
which does contain specification for a base. The righthand ... is
a program:
~HOLDING WHICH_BASE := N ;
~DO <*F*>;
~ENDHOLD
This rule invokes F after putting the correct base into WHICH_BASE.
We use the ~HOLDING construct because we don't want to have a permanent
effect on the global variable WHICH_BASE. We want merely a temporary
effect, long enough to cover the invocation of F. After the ENDHOLD,
WHICH_BASE goes back to its original value, e.g., ten. (Sections
21.4.2.2 or 22.1.10 or 22.2.2 tell more).
(This use of HOLDING is equivalent to:
OLD := WHICH_BASE; "Save the original value"
WHICH_BASE:= N;
<*F*>;
WHICH_BASE:= OLD; "Restore original value" )
2.4.1
Another Example Of Top-Down Context
The following example probably has no application, but it will further
illustrate top-down context. More realistic examples will follow in
Section 3.3.
For now, let's introduce a new, odd meaning for parentheses. Let's
suppose that parentheses not only imply a grouping, but that they also
change all numbers appearing between the parentheses. We would like
each pair of enclosing parentheses to cause all numbers within them
to be multiplied by a factor of ten. That is, we would like the
following printouts upon invoking semantics:
5 appears as 5
(5) appears as 50
((5)) appears as 500
1+(2*(3)) appears as (1+(20*300))
We change two rules:
<NUMBER:n> -> <ATOM: atomize(n) >
( <FORM:f> ) -> <ATOM: f >
We change the first rule so as to write numbers multiplied by some
power of 10, a value that we ~presume is in the new variable
THE_FACTOR:
<NUMBER:n> -> <ATOM: //[n;]
WRITE( n * THE_FACTOR );
\\ >
(We've abandoned the ATOMIZE function, but we've replaced the call
to ATOMIZE directly by what we'd otherwise put into a modified
rendition of ATOMIZE). The semantics of the <ATOM> is a BASIC_PROCESS
whose action is to write out N times THE_FACTOR.
We must declare the top-down context variable THE_FACTOR. We declare
it now:
VAR THE_FACTOR = INT ;
Prior to invoking any <ATOM>, we must set THE_FACTOR.
The updated parentheses rule sets THE_FACTOR:
( <FORM:f> ) ->
<ATOM: //[f;]
HOLDING THE_FACTOR:= THE_FACTOR*10;
DO <*f*>;
ENDHOLD
\\ >
This //...\\ in the <ATOM> is a BASIC_PROCESS (as is demanded by the
part-of-speech ATOM). Its action is to invoke F (the <FORM> between
the parentheses) under the illusion that THE_FACTOR is ten times
greater.
Once again, we use the HOLDING construct to
assign the new value into THE_FACTOR: We want this effect to exist
only during the invocation <*F*>. THE_FACTOR provides the
communication from this parentheses rule down to the semantics of
the <ATOM>, which prints numbers.
With this rule, we haven't taken the time to make up a new function,
say
DEFINE PAREN( F:BASIC_PROCESS ) = BASIC_PROCESS: ... ENDDEFN
We've written the body of the function instead of a call to the
function.
Before we start any of this, let's set THE_FACTOR's default value,
(the value that will reign outside any parentheses):
THE_FACTOR:= 1 ;
2.4.2
Exercises
1) What value will THE_FACTOR contain when we actually print out
the 5 in
(2+5)*3 ?
What about in
1+2*(3+(4)+5)
or
1+2*(3+(4+5)) ?
2) How will 1+2*(3+(4+5)) appear upon invocation of semantics?
3) Suppose we didn't use the HOLDING construct in the parentheses
rule. Suppose we wrote instead:
( <FORM:f> ) ->
<ATOM: //[f;]
THE_FACTOR:= THE_FACTOR*10;
<*f*>;
\\ >
How will (1)+(2) appear? How about 1+(2)+3?
What if we invoke the semantics of 1+(2+3) and then invoke
the semantics of 1? What will the lone 1 appear as? What if
we then invoke the semantics of 2+(3)? What will we see?
4) Modify the semantics of the <ATOM> in the previous excercise
so that without the HOLDING construct, THE_FACTOR will appear
on exit to contain the same value as it had upon entrance.
5) Rewrite the parentheses rule and the "+" rule (SUM) so that
within parentheses, "+" prints out its operands swapped, i.e.,
1+2 appears as (1+2)
1+(2+3) appears as (1+(3+2))
1+((2+3)) appears as (1+(3+2))
1+(2+(3+4)) appears as (1+((4+3)+2))
That is, the operand order is reversed for any expression
enclosed in one or more parentheses pairs. You will need to
declare a new global as follows:
VAR INSIDE_PARENS = BOOL ;
This is a Boolean variable. It can be assigned the values
TRUE and FALSE, and it can be used in the IF-THEN-ELSE
construct, e.g.,
IF INSIDE_PARENS THEN ...
ELSE ... FI
(The FI is part of the IF-THEN-ELSE notation, as shown in
Section 21.4.2.3 or 22.2.3).
First ask yourself which two rules need to be modified.
6) Instead of having parentheses multiply by ten everything
inside them, have them instead subtract one. We want
1+(3+4) to appear as (1+(2+3))
1+(3+(4)) to appear as (1+(2+2))
Modify two rules to make this so. You
can use the variable THE_FACTOR, although a better variable
name would be THE_DEBIT.
7) Consider now only the WHICH_BASE top-down context variable.
Consider the new rule:
<ATOM:a> IN BASE <NUMBER:n> ->
<ATOM: //[a;n;]
HOLDING WHICH_BASE:= n;
DO <*a*>;
ENDHOLD
\\ >
This rule allows an <ATOM> to be augmented with a new base
specification for print out. What will the following appear
as:
a) 5 IN BASE 2
b) 5+6 IN BASE 2
c) (5+6) IN BASE 2
d) 5+(6 IN BASE 2)
e) 5+6 IN BASE 2 * 3 IN BASE 3
f) 5 IN BASE 2 IN BASE 3
g) 5+6 IN BASE 2 IN BASE 3
It will be helpful to write down the derivation for each of
these expressions.
Suppose we change the new rule so that <FORM> appears instead
of <ATOM>:
<FORM:a> IN BASE <NUMBER:n> -> <FORM: ... >
(The "..." is unchanged). Which of the above formulas can
still be viewed as a <FORM>? How do those legal <FORM>s
appear when their semantics are invoked?
More practical examples of top-down context will appear in the next
chapter.